题目内容
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .
.

(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() ,
,![]() ,
,![]() 中恰有一点是其它两点所连线段的中点(三点重合除外),则称
中恰有一点是其它两点所连线段的中点(三点重合除外),则称![]() ,
,![]() ,
,![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() ,
,![]() ,
,![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
【答案】(1)B(0,2),![]() ;(2)①点M的坐标为(
;(2)①点M的坐标为(![]() ,0)或M(
,0)或M(![]() ,0);②m=-1或m=
,0);②m=-1或m=![]() 或m=
或m=![]() .
.
【解析】
试题分析:(1) 把点![]() 代入
代入![]() 求得c值,即可得点B的坐标;抛物线
求得c值,即可得点B的坐标;抛物线![]() 经过点
经过点![]() ,即可求得b值,从而求得抛物线的解析式;(2)由
,即可求得b值,从而求得抛物线的解析式;(2)由![]() 轴,M(m,0),可得N(
轴,M(m,0),可得N(![]() ),①分∠NBP=90°和∠BNP =90°两种情况求点M的坐标;②分N为PM的中点、P为NM的中点、M为PN的中点3种情况求m的值.
),①分∠NBP=90°和∠BNP =90°两种情况求点M的坐标;②分N为PM的中点、P为NM的中点、M为PN的中点3种情况求m的值.
试题解析:
(1)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ,解得c=2
,解得c=2
∴B(0,2),
∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() ,∴b=
,∴b=![]()
∴抛物线的解析式为![]() ;
;
(2)∵![]() 轴,M(m,0),∴N(
轴,M(m,0),∴N(![]() )
)
①有(1)知直线AB的解析式为![]() ,OA=3,OB=2
,OA=3,OB=2
∵在△APM中和△BPN中,∠APM=∠BPN, ∠AMP=90°,
若使△APM中和△BPN相似,则必须∠NBP=90°或∠BNP =90°,
分两种情况讨论如下:
(I)当∠NBP=90°时,过点N作NC![]() 轴于点C,
轴于点C,
则∠NBC+∠BNC=90°,NC=m,
BC=![]()
∵∠NBP=90°,∴∠NBC+∠ABO=90°,
∴∠BNC=∠ABO,
∴Rt△NCB∽ Rt△BOA
∴![]() ,即
,即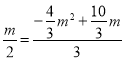 ,解得m=0(舍去)或m=
,解得m=0(舍去)或m=![]()
∴M(![]() ,0);
,0);
(II)当∠BNP=90°时, BN![]() MN,
MN,
∴点N的纵坐标为2,
∴![]()
解得m=0(舍去)或m=![]()
∴M(![]() ,0);
,0);
综上,点M的坐标为(![]() ,0)或M(
,0)或M(![]() ,0);
,0);
②m=-1或m=![]() 或m=
或m=![]() .
.