题目内容
【题目】在平面直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是（﹣3，2）．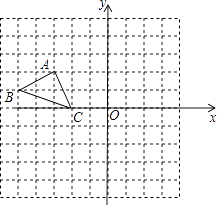
（1）将△ABC向右平移6个单位长度，再向下平移4个单位长度，得到△A'B′C′．请画出平移后的△A′B′C′，并写出点的坐标A′、B、C′；
（2）求出△A′B′C′的面积；
（3）若连接AA′、CC′，则这两条线段之间的关系是 ．
【答案】
（1）3，﹣2；1，﹣3；4，﹣4
（2）
解：S△A′B′C′=3×2﹣ 
×2×1﹣ ×1×2﹣ ×1×3
=6﹣1﹣1﹣ 
= 
（3）AA′∥CC′，AA′=CC′
【解析】解：（1）由图可知，A′（3，﹣2）、B′（1，﹣3）、C′（4，﹣4）．
所以答案是：3，﹣2；1，﹣3；4，﹣4；（3）由图形平移的性质可知，AA′∥CC′，AA′=CC′．
所以答案是：AA′∥CC′，AA′=CC′．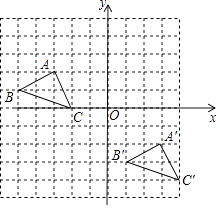
【考点精析】掌握三角形的面积和平移的性质是解答本题的根本，需要知道三角形的面积=1/2×底×高；①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化；②经过平移后，对应点所连的线段平行（或在同一直线上）且相等．
练习册系列答案
相关题目
【题目】某学习小组9名学生参加“数学竞赛”，他们的得分情况如表：
人数（人） | 1 | 3 | 4 | 1 |
分数（分） | 80 | 85 | 90 | 95 |
那么这9名学生所得分数的众数和中位数分别是（ ）
A.90，90
B.90，85
C.90，87.5
D.85，85
