题目内容
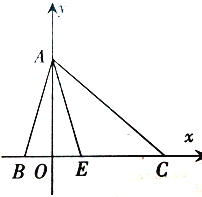
【题目】如图,等边△ABC中,点D在延长线上,CE平分∠ACD,且CE=BD.说明:△ADE是等边三角形.
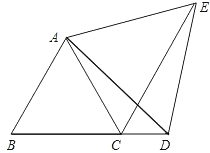
【答案】详见解析.
【解析】试题分析:
要证△ADE为等边三角形,可以先证它为等腰三角形,再证该等腰三角形的一个内角为60°. 综合分析已知条件可知,可以利用△ABD和△ACE全等证明AD=AE. 根据已知条件和等边三角形的性质,不难证明∠B=∠ACE,进而利用SAS证明△ABD和△ACE全等. 利用全等三角形的性质可以得到△ADE是等腰三角形. 利用全等三角形的性质,通过相关角之间的和差关系,不难证明∠DAE=∠BAC=60°,从而证明△ADE为等边三角形.
试题解析:
证明:∵△ABC为等边三角形,
∴∠B=∠ACB=∠BAC=60°,AB=AC.
∵∠ACB=60°,
∴∠ACD=180°-∠ACB=180°-60°=120°,
∵CE平分∠ACD,
∴![]() .
.
∴∠B=∠ACE.
∵在△ABD和△ACE中,
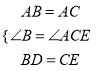 ,
,
∴△ABD≌△ACE (SAS),
∴AD=AE,∠BAD=∠CAE.
∵∠BAD=∠CAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAC=∠DAE=60°.
∵∠DAE=60°,AD=AE,
∴△ADE为等边三角形.

练习册系列答案
相关题目
【题目】如图,截止5月1日浙江抗击新冠肺炎部分城市治愈总人数统计表,下列说法错误的是( )
城市 | 杭州 | 宁波 | 金华 | 温州 | 台州 |
治愈总人数 | 181 | 157 | 55 | 503 | 146 |
A.金华治愈总人数最少B.杭州治愈总人数最多
C.温州治愈总人数503人D.宁波治愈总人数比台州多