题目内容
【题目】(1)阅读理解
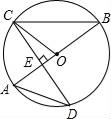
利用旋转变换解决数学问题是一种常用的方法.如图1,点P是等边三角形ABC内一点,PA=1,PB=![]() ,PC=2.求∠BPC的度数.
,PC=2.求∠BPC的度数.
为利用已知条件,不妨把△BPC绕点C顺时针旋转60°得△AP′C,连接PP′,则PP′的长为_____;在△PAP′中,易证∠PAP′=90°,且∠PP′A的度数为_____,综上可得∠BPC的度数为_____;
(2)类比迁移
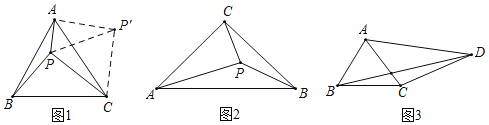
如图2,点P是等腰Rt△ABC内的一点,∠ACB=90°,PA=2,PB=![]() ,PC=1,求∠APC的度数;
,PC=1,求∠APC的度数;
(3)拓展应用
如图3,在四边形ABCD中,BC=3,CD=5,AB=AC=![]() AD.∠BAC=2∠ADC,请直接写出BD的长.
AD.∠BAC=2∠ADC,请直接写出BD的长.
【答案】(1)2;30°;90°;(2)∠APC=90°;(3)BD=![]() .
.
【解析】
(1)由旋转性质、等边三角形的判定可知△CP′P是等边三角形,由等边三角形的性质知∠CP′P=60°,根据勾股定理逆定理可得△AP′P是直角三角形,继而可得答案.
(2)如图2,把△BPC绕点C顺时针旋转90°得△AP'C,连接PP′,同理可得△CP′P是等腰直角三角形和△AP′P是直角三角形,所以∠APC=90°;
(3)如图3,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,根据勾股定理求CG的长,就可以得BD的长.
解:(1)把△BPC绕点C顺时针旋转60°得△AP'C,连接PP′(如图1).

由旋转的性质知△CP′P是等边三角形;
∴P′A=PB=![]() 、∠CP′P=60°、P′P=PC=2,
、∠CP′P=60°、P′P=PC=2,
在△AP′P中,∵AP2+P′A2=12+(![]() )2=4=PP′2;
)2=4=PP′2;
∴△AP′P是直角三角形;
∴∠P′AP=90°.
∵PA=![]() PC,
PC,
∴∠AP′P=30°;
∴∠BPC=∠CP′A=∠CP′P+∠AP′P=60°+30°=90°.
故答案为:2;30°;90°;
(2)如图2,把△BPC绕点C顺时针旋转90°得△AP'C,连接PP′.
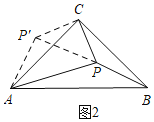
由旋转的性质知△CP′P是等腰直角三角形;
∴P′C=PC=1,∠CPP′=45°、P′P=![]() ,PB=AP'=
,PB=AP'=![]() ,
,
在△AP′P中,∵AP'2+P′P2=(![]() )2+(
)2+(![]() )2=2=AP2;
)2=2=AP2;
∴△AP′P是直角三角形;
∴∠AP′P=90°.
∴∠APP'=45°
∴∠APC=∠APP'+∠CPP'=45°+45°=90°
(3)如图3,
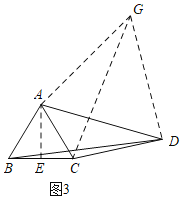
∵AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=2AB,
∴DG=2BC=6,
过A作AE⊥BC于E,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG=![]() ,
,
∴BD=CG=![]() .
.

 一线名师权威作业本系列答案
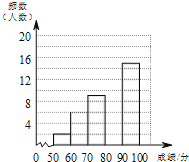
一线名师权威作业本系列答案【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?