题目内容
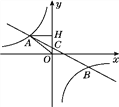
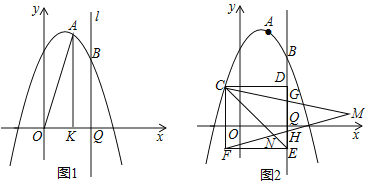
【题目】已知:如图,二次函数y=ax2+bx+![]() 的图象经过点A(2,6)和B(4,4),直线l经过点B并与x轴垂直,垂足为Q.
的图象经过点A(2,6)和B(4,4),直线l经过点B并与x轴垂直,垂足为Q.
(1)求二次函数的表达式;
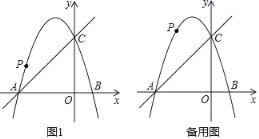
(2)如图1,作AK⊥x轴,垂足为K,连接AO,点R是直线1上的点,如果△AOK与以O,Q,R为顶点的三角形相似,请直接写出点R的纵坐标;
(3)如图2,正方形CDEF的顶点C是第二象限抛物线上的点,点D,E在直线1上,以CF为底向右做等腰△CFM,直线l与CM,FM的交点分别是G,H,并且CG=GM,FH=HM,连接CE,与FM的交点为N,且点N的纵坐标是﹣1.
求:①tan∠DCG的值;
②点C的坐标.
【答案】(1)y=﹣![]() ;(2)点R的纵坐标为12,﹣12,
;(2)点R的纵坐标为12,﹣12,![]() 或﹣
或﹣![]() ;(3)①tan∠DCG的值是
;(3)①tan∠DCG的值是![]() ,②点C坐标为(﹣1,3).
,②点C坐标为(﹣1,3).
【解析】
(1)将点A(2,6)和B(4,4)代入抛物线解析式,得方程组,解得a和b,再代回原解析式即可;
(2)设点R的纵坐标为n,则QN=|n|,分两种情况,根据相似关系列比例式即可解得;
(3)①由三角形的中位线,及证Rt△CDG≌Rt△FEH (HL)可解;
②先根据点C在抛物线上,设其横坐标为m,然后用其分别表示出相关点的坐标,并表示出直线CE,再根据△CFN∽△EHN,及相似三角形对应边上的高之比也等于相似比,从而建立关于m的方程,解之,然后代回点C即可.
(1)将点A(2,6)和B(4,4)代入y=ax2+bx+![]() 得:
得:
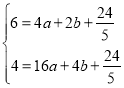 ,解得
,解得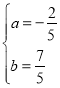
∴二次函数的表达式为y=![]() .
.
(2)∵A(2,6),AK⊥x轴,
∴K(2,0),
△AOK中,OK=2,AK=6,OA=![]() ,
,
△OQR中,OQ=4,
设点R的纵坐标为n,则QN=|n|,
如果△AOK与以O,Q,R为顶点的三角形相似,有两种情况:
①![]() ,则n=±12;
,则n=±12;
②![]() ,则
,则![]() ,从而n=±
,从而n=±![]() .
.
答:点R的纵坐标为,12,﹣12,![]() 或﹣
或﹣![]() .
.
(3)①∵CG=GM,FH=HM,
∴GH∥CF,GH=![]() CF,
CF,
∵等腰△CFM,
∴CG=FH,
∵CDEF为正方形,
∴CD=EF,∠CDG=∠FEH=90°,
∴Rt△CDG≌Rt△FEH (HL),
∴DG=EH,
∵GH=![]() CF,
CF,
∴DG=EH=![]() CF=
CF=![]() CD,
CD,
∴tan∠DCG=![]() =
=![]() ,
,
答:tan∠DCG的值是![]() .
.
②∵C是第二象限抛物线y=![]() 上的点,
上的点,
∴设点C坐标为(m,![]() ),则DC=4﹣m,
),则DC=4﹣m,
∴F(m,![]() ﹣4+m),即F(m,
﹣4+m),即F(m,![]() ),
),
∴E(4,![]() ),
),
∵CDEF为正方形,
∴∠DEC=45°,
故可设CE解析式为:y=﹣x+b,将点E坐标代入得b=![]() .
.
∴CE解析式为:y=﹣x﹣![]() ,
,
∵点N的纵坐标是﹣1,
∴﹣1=﹣x﹣![]() ,x=﹣
,x=﹣![]() ,
,
∴点N坐标为(﹣![]() ,﹣1),
,﹣1),
∵CDEF为正方形,
∴CF∥EH,
∴△CFN∽△EHN,
∵tan∠DCG=![]() =
=![]() ,DG=EH,CD=CF,
,DG=EH,CD=CF,
∴![]() ,则EH边上的高与CF边上的高的比值也为
,则EH边上的高与CF边上的高的比值也为![]() ,
,
∴![]() ,
,
化简得:﹣2m2+11m+13=0,解得m=![]() (舍)或m=﹣1,
(舍)或m=﹣1,
∴点C坐标为(﹣1,3).
答:点C坐标为(﹣1,3).

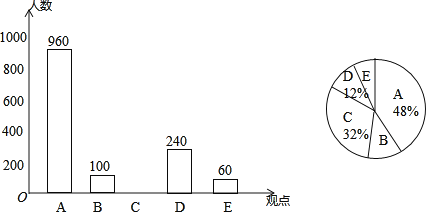
【题目】某公益机构为了解市民使用“手机阅读”的情况,对部分市民进行了随机问卷调查(问卷调查表如左图所示),并将调查结果绘制成两副统计图(均不完整)
您如何看待手机阅读问卷调查表 您好!请在表格中选择一项您最认同的观点,在其后面空格内打“√”,非常感谢您的配合. | ||
选项 | 观点 | 您的选择 |
A | 更新及时 | □ |
B | 阅读成本低 | □ |
C | 不利于人际交往 | □ |
D | 内容丰富 | □ |
E | 其他 | □ |
(1)本次接受调查的总人数是______人.
(2)请将条形统计图补充完整.
(3)在扇形统计图中,表示观点B的扇形的圆心角度数为______度.
(4)根据上述调查结果,请估计在2万名市民中,认为手机阅读“内容丰富“的大约有______人.