题目内容
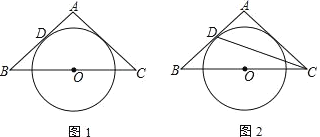
【题目】如图1,△ABC是等腰三角形,O是底边BC中点,腰AB与⊙O相切于点D
(1)求证:AC是⊙O的切线;
(2)如图2,连接CD,若tan∠BCD=![]() ,⊙O的半径为
,⊙O的半径为![]() ,求BC的长.
,求BC的长.
【答案】(1)证明见解析;(2)BC=6.
【解析】
(1)连接OD,作OF⊥AC于F,如图,利用等腰三角形的性质得AO⊥BC,AO平分∠BAC,再根据切线的性质得OD⊥AB,然后利用角平分线的性质得到OF=OD,从而根据切线的判定定理得到结论;
(2)过D作DF⊥BC于F,连接OD,根据三角函数的定义得到![]() ,设DF=
,设DF=![]() a,OF=x,则CF=4a,OC=4a-x根据相似三角形的性质得到
a,OF=x,则CF=4a,OC=4a-x根据相似三角形的性质得到![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
(1)证明:连接OD,OA,作OF⊥AC于F,如图,
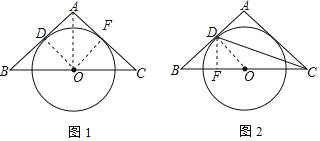
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO⊥BC,AO平分∠BAC,
∵AB与⊙O相切于点D,
∴OD⊥AB,
而OF⊥AC,
∴OF=OD,
∴AC是⊙O的切线;
(2)过D作DF⊥BC于F,连接OD,
∵tan∠BCD=![]() ,
,
∴![]() ,
,
设DF=![]() a,OF=x,则CF=4a,OC=4a﹣x,
a,OF=x,则CF=4a,OC=4a﹣x,
∵O是底边BC中点,
∴OB=OC=4a﹣x,
∴BF=OB﹣OF=4a﹣2x,
∵OD⊥AB,
∴∠BDO=90°,
∴∠BDF+∠FDO=90°,
∵DF⊥BC,
∴∠DFB=∠OFD=90°,∠FDO+∠DOF=90°,
∴∠BDF=∠DOF,
∴△DFO∽△BFD,
∴![]() ,
,
∴![]() ,
,
解得:x1=x2=a,
∵⊙O的半径为![]() ,
,
∴OD=![]() ,
,
∵DF2+FO2=DO2,
∴(![]() x)2+x2=(
x)2+x2=(![]() )2,
)2,
∴x1=x2=a=1,
∴OC=4a﹣x=3,
∴BC=2OC=6.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目