题目内容
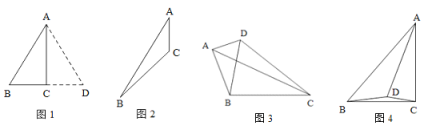
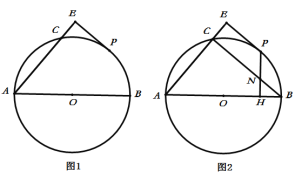
【题目】如图1,![]() 是
是![]() 的直径,
的直径,![]() 是弦,点
是弦,点![]() 是
是![]() 的中点,
的中点,![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
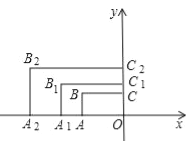
(2)如图2,作![]() 于
于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)8
【解析】
(1)连接BC、OP,由AB是⊙O的直径、PE⊥AE知PE∥BC,根据点P是![]() 的中点知OP⊥BC,即可得OP⊥PE;
的中点知OP⊥BC,即可得OP⊥PE;
(2)由(1)知,四边形PECQ是矩形,从而可设PE=CQ=BQ=x,根据勾股定理求得BN的长,先证△BHN∽△BQO得![]() ,表示出BO、OQ的长,再证△PQN∽△BHN得
,表示出BO、OQ的长,再证△PQN∽△BHN得![]() ,即
,即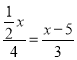 ,求出x即可.
,求出x即可.
解:(1)如图1,连接BC、OP,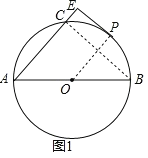
∵AB是⊙O的直径,
∴∠ACB=90°,即BC⊥AE,
又∵PE⊥AE,
∴PE∥BC,
∵点P是![]() 的中点,
的中点,
∴OP⊥BC,
∴OP⊥PE,
∴PE是⊙O的切线;
(2)如图2,连接OP,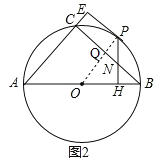
由(1)知,四边形PECQ是矩形,
∴设PE=CQ=BQ=x,
∵NH=3,BH=4,PH⊥AB,
∴BN=5,
∵∠B=∠B,∠BHN=∠BQO=90°,
∴△BHN∽△BQO,
∴![]() ,即
,即![]() ,
,
解得:BO=![]() ,OQ=
,OQ=![]() ,
,
∴PQ=PO-OQ=BO-OQ=![]() ,
,
∵∠PNQ=∠BNH,∠PQN=∠BHN=90°,
∴△PQN∽△BHN,
∴![]() ,
,
即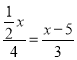 ,
,
解得:![]() ,
,
∴PE=8.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目