题目内容
【题目】二次函数y=﹣![]() x2+bx+c的图象与直线y=﹣
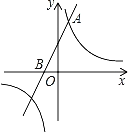
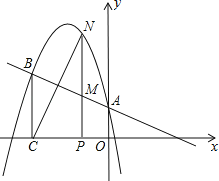
x2+bx+c的图象与直线y=﹣![]() x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为C(﹣3,0).
(1)填空:b=_____,c=_____.
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
【答案】(1)![]() ,1;(2)MN的最大值
,1;(2)MN的最大值
【解析】
(1)由一次函数解析式求得点A、B的坐标,然后将其代入二次函数解析式,即利用待定系数法确定函数解析式;(2)设M的横坐标是x,则根据M和N所在函数的解析式,即可利用x表示出M、N的坐标,利用x表示出MN的长,利用二次函数的性质求解;(3)BM与NC互相垂直平分,即四边形BCMN是菱形,则BC=MC,据此即可列方程,求得x的值,从而得到N的坐标;
解:
(1)由直线y=﹣![]() x+1得到:A(0,1),
x+1得到:A(0,1),
把x=﹣3代入y=﹣![]() x+1得到:y=﹣
x+1得到:y=﹣![]() ×(﹣3)+1=
×(﹣3)+1=![]() .
.
故B(﹣3,![]() ).
).
将A、B的坐标分别代入y=﹣![]() x2+bx+c,得
x2+bx+c,得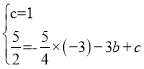 ,
,
解得b=![]() ,c=1;
,c=1;
(2)设N(m,﹣![]() m2
m2![]() m+1) ,
m+1) ,
则,M,P点的坐标分别是(m,﹣![]() m+1),(m,0),
m+1),(m,0),
∴MN=(﹣![]() m2
m2![]() m+1)﹣(﹣
m+1)﹣(﹣![]() m2+1) ,
m2+1) ,
=﹣![]() m2﹣
m2﹣![]() m
m
=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
∴当m=﹣![]() 时,MN的最大值为
时,MN的最大值为![]() ;
;
(3)连接MN,BN,由BM与NC互相垂直平分,
∴四边形BCMN是菱形
由BC∥MN,
∴MN=BC,且BC=MC,
而BC=﹣![]() ×(﹣3)+1=
×(﹣3)+1=![]() ,
,
即:﹣![]() m2﹣
m2﹣![]() m=
m=![]() ,
,
且(﹣![]() m+1)2+(m+3) 2=
m+1)2+(m+3) 2=![]() ,
,
解得:m=﹣1;
故当N(﹣1,4)时,BM与NC互相垂直平分.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】某校为了对甲,乙两名同学进行学生会主席的竞选考核、召开了一次竞选答辩及民主测评会.由A,B,C,D,E五位教师评委对竞选答辩进行评分,并选出20名学生代表参加民主投票.竞选答辩的结果如下表所示:
评委 得分 选手 | A | B | C | D | E |
甲 | 92 | 88 | 90 | 94 | 96 |
乙 | 84 | 86 | 90 | 93 | 91 |

民主投票的结果为:甲8票,乙12票.
根据以上信息解答下列问题:
(1)甲,乙两人的竞选答辩得分分别是多少?
(2)如果综合得分=竞选答辩得分+民主投票得分,那么,甲,乙两人谁当选学生会主席?
(3)如果综合得分=竞选答辩得分![]() 民主投票得分
民主投票得分![]() ,那么,当
,那么,当![]() 时,甲,乙两人谁当选学生会主席?
时,甲,乙两人谁当选学生会主席?
【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
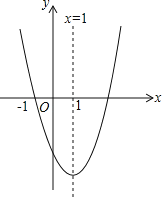
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;
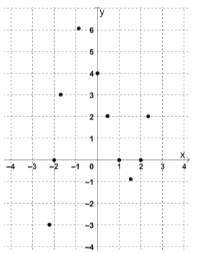
观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .