题目内容
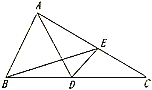
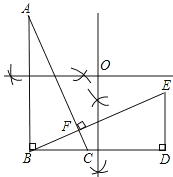
【题目】如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE![]() AC,与BD的垂线DE交于点E,
AC,与BD的垂线DE交于点E,
(1)求证:△ABC≌△BDE
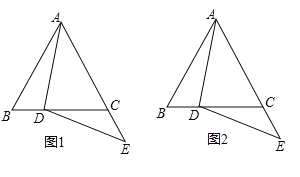
(2)三角形BDE可由三角形ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法)
【答案】(1)见解析
(2)见解析
【解析】
三角形内角和定理,全等三角形的判定,作图(旋转变换),线段垂直平分线的性质.
(1)利用已知得出∠A=∠DBE,从而利用ASA得出△ABC≌△BDE即可.
证明:在Rt△ABC中,∵∠ABC=90°,
∴∠ABE+∠DBE=90°.
∵BE⊥AC,
∴∠ABE+∠A=90°.
∴∠A=∠DBE.
∵DE是BD的垂线,
∴∠D=90°.
在△ABC和△BDE中,
∵∠A=∠DBE ,AB=DB ,∠ABC=∠D,
∴△ABC≌△BDE(ASA).
(2)利用垂直平分线的性质可以作出,或者利用正方形性质得出旋转中心也可.
如图,点O就是所求的旋转中心.

练习册系列答案
相关题目