Question

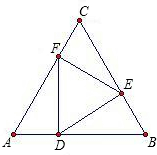
如图，在边长为1的等边△ABC中，中线AD与中线BE相交于点O，则OA长度为______．

Answer 1

∵△ABC是等边三角形，AD、BE为中线；
∴BD=AE=

1

2

，∠ABE=∠BAD=30°，∠AEB=∠ADB=90°；
∴AD=BE=AB•sin60°=

3

2

；
在Rt△BOD中，BD=

1

2

，∠DBO=30°；
∴OD=BD•tan30°=

1

2

×

3

3

=

3

6

；
∴OA=AD-OD=

3

2

-

3

6

=

3

3

．
故OA的长度为

3

3

．