题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴左侧抛物线交于点
轴左侧抛物线交于点![]() ,直线
,直线![]() 与
与![]() 轴右侧抛物线交于点
轴右侧抛物线交于点![]() .
.
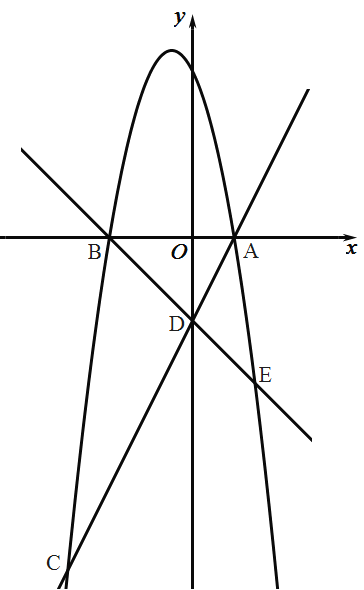
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,求
上方抛物线上一动点,求![]() 面积的最大值;
面积的最大值;
(3)点![]() 是抛物线上一动点,点
是抛物线上一动点,点![]() 是抛物线对称轴上一动点,请直接写出以点
是抛物线对称轴上一动点,请直接写出以点![]() 为顶点的四边形是平行四边形时点
为顶点的四边形是平行四边形时点![]() 的坐标.
的坐标.
【答案】(1) ![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)直接利用待定系数法,即可求出解析式;
(2)先求出点C的坐标,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设P
,设P![]() ,则
,则![]() ,则得到线段PQ的长度,然后利用三角形面积公式,即可求出答案;
,则得到线段PQ的长度,然后利用三角形面积公式,即可求出答案;
(3)先求出直线BD,然后得到点E的坐标,由以点![]() 为顶点的四边形是平行四边形,设点M为(m,
为顶点的四边形是平行四边形,设点M为(m,![]() ),则可分为三种情况进行①当CN与ME为对角线时;②当CE与MN为对角线时;③当EN与CM为对角线时;由平行四边形对角线互相平分,即可得到m的值,然后求出点M的坐标.
),则可分为三种情况进行①当CN与ME为对角线时;②当CE与MN为对角线时;③当EN与CM为对角线时;由平行四边形对角线互相平分,即可得到m的值,然后求出点M的坐标.
解:(1)把![]() 代入中得
代入中得![]() ,
,
![]()
解得![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
(2)由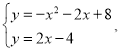
得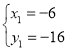 ,
, ,
,
![]() .
.
过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,
,
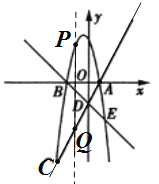
设![]() ,则
,则![]() ,
,
![]() ,
,
![]()
![]()
![]() .
.
![]() 当
当![]() 时,
时,![]() ;
;
∴![]() 面积的最大值为64.
面积的最大值为64.
(3)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴点D的坐标为:(0,![]() ),
),
∵点B为(![]() ),
),
∴直线BD的方程为:![]() ;
;
联合抛物线与直线BD,得:
![]() ,
,
解得: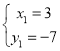 或
或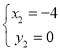 (为点B),
(为点B),
∴点E的坐标为:(3,![]() );
);
∵抛物线![]() 的对称轴为:
的对称轴为:![]() ,
,
∴点N的横坐标为![]() ;
;
∵以点![]() 为顶点的四边形是平行四边形,且点C(
为顶点的四边形是平行四边形,且点C(![]() ),点E(3,
),点E(3,![]() ),
),
设点M为(m,![]() ),则可分为三种情况进行
),则可分为三种情况进行
①当CN与ME为对角线时,由平行四边形对角线互相平分,
∴![]() ,
,
解得:![]() ;
;
∴点M的纵坐标为:![]() ,
,
∴点M的坐标为:(![]() );
);
②当CE与MN为对角线时,由平行四边形对角线互相平分,
∴![]() ,
,
解得:![]() ,
,
∴点M的纵坐标为:![]() ,
,
∴点M的坐标为:(![]() );
);
③当EN与CM为对角线时,由平行四边形对角线互相平分,
∴![]() ,
,
解得:![]() ,
,
∴点M的纵坐标为:![]() ;
;
∴点M的坐标为:(![]() );
);
综合上述,点![]() 的坐标为:
的坐标为:![]() 或
或![]() .
.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案