Question

【题目】已知，如图，在△ ABC中，AD，AE分别是 △ ABC的高和角平分线，若∠B=30°，∠C=50°.

(1)求∠DAE的度数.

(2)试写出 ∠DAE与∠C-∠B有何关系?(不必证明)

Answer 1

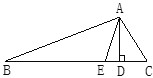
【答案】（1）10°；（2）∠C-∠B=2∠DAE．

【解析】

（1）根据三角形内角和等于180°求出∠BAC的度数，然后根据AE是角平分线求出∠CAE的度数，在△ACD中，利用直角三角形两锐角互余求出∠CAD的度数，两角相减即可求解；
（2）同（1）的思路整理即可．

（1）∵∠B=30°，∠C=50°，

∴∠BAC=180°-30°-50°=100°．

∵AE是∠BAC的平分线，

∴∠BAE=50°．

在Rt△ABD中，∠BAD=90°-∠B=60°，

∴∠DAE=∠BAD-∠BAE=60°-50=10°；

（2）∠C-∠B=2∠DAE．