题目内容
【题目】我们把两个大小相等,形状相同的两个三角形称之为全等三角形,如果两个三角形仅仅是形状相同,我们可以称之为相似三角形,如图①△ABC与△DEF形状相同,我们就可以说△ABC 与△DEF相似,记作△ABC∽△DEF,点A与点D、点B与点E、点C与点F分别是对应点。下面我们就相似三角形的知识进行一些简单的探索。

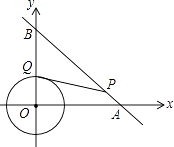
(1)观察下列图②两组图形,相似的一组是 。

(2)如图③,小明用一张纸遮住了3个三角形的一部分,你是可以画出这3个三角形的。

提出问题:①如图,如果∠A=∠C,∠B=∠D,AB=CD,那么第一个三角形与第二个三角形全等吗?你的判断是 ,(填“是”或“否”)判断的依据是 。
②如图,如果∠A=∠E,∠B=∠F,2AB=EF,那么第一个三角形与第三个三角形相似吗?你的判断是 ,(填“是”或“否”)
(3)由(1)、(2)你可以得出的结论是:有 个角分别相等的两个三角形相似。
(4)用(3)的结论解决下面两个问题.
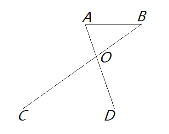
①已知:如图,AB∥CD。AD与BC相交于点O,试说明△ABO∽△DCO。
②已知:如图,在△ABC中,点D、E、F分别在边BC、AB、AC上,∠B=∠C=∠EDF,试说明△BDE∽△CFD.

【答案】(1)第一组;(2)① 是 , 角边角; ②是; (3)2 ;(4)①见解析;②见解析
【解析】
(1)根据相似三角形的定义进行判断;
(2) ①根据全等三角形的判定即可解答;
②根据相似三角形的定义进行判断;
(3)形状不变,角的度数不变,三角形中只要两个角相等,则第3个角也相等;
(4)①利用两角对应相等的两三角形相似即可解答;
②证明两组对角相等即可.
(1)第一组;
(2)①是,角边角;
②是;
(3)2 ;
(4)①证明:
∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△ABO∽△DCO,
②证明:
∵∠B+∠BED+∠BDE=180°,∠BDE+∠EDF+∠CDF=180°,
且∠B=∠EDF,
∴∠BED=∠CDF,
又∵∠B=∠C,
∴△BDE∽△CFD.