题目内容
已知∠AOB=45°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1、O、P2三点构成的三角形是 ( )
| A.直角三角形 | B.等腰三角形 | C.等边三角形 | D.等腰直角三角形 |
D.
试题分析:如图,连接OP,
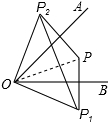
∵P1与P关于OB对称,P2与P关于OA对称,
∴OP=OP1=OP2,∠BOP1=∠BOP,∠AOP2=∠AOP,
∴∠P1OP2=∠BOP1+∠BOP+∠AOP2+∠AOP=2(∠BOP+∠AOP)=2∠AOB,
∵∠AOB=45°,
∴∠P1OP2=2×45°=90°,
∴P1,O,P2三点构成的三角形是等腰直角三角形.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目


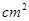 和4
和4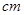 .
.