题目内容
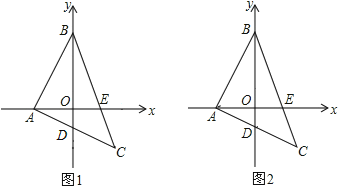
【题目】已知二次函数y=ax2+bx+c的图象如图所示，OA=OC，则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式：①
=﹣1；②ac+b+1=0；③abc＞0；④a﹣b+c＞0．其中正确的个数是（ ）
A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】
此题可根据二次函数的性质，结合其图象可知：a＞0，﹣1＜c＜0，b＜0，再对各结论进行判断即可得答案．
①由图象知抛物线顶点纵坐标为﹣1，即
=﹣1，故①正确；
②设C（0，c），则OC=|c|，
∵OA=OC=|c|，∴A（c，0）代入抛物线得ac2+bc+c=0，又c≠0，
∴ac+b+1=0，故②正确；
③从图象中易知a＞0，b＜0，c＜0，则abc＞0，故③正确；
④当x=﹣1时y=a﹣b+c，由图象知（﹣1，a﹣b+c）在第二象限，
∴a﹣b+c＞0，故④正确，
故选A．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
