Question

【题目】如图，在等腰三角形ABC中，∠ACB=90°，AC=BC=2cm，点M（不与A、B重合），从点A出发沿AB方向以cm/s的速度向终点B运动．在运动过程中，过点M作MN⊥AB，交射线BC于点N，以线段MN为直角边作等腰直角三角形MNQ，且∠MNQ=90°（点B、Q位于MN两侧）．设△MNQ与△ABC重叠部分图形面积为S（cm2），点M的运动时间为t（s）．

（1）用含t的代数式表示线段MN的长，MN= ．

（2）当点N与点C重合时，t= ．

（3）求S与t之间的函数关系式．

Answer 1

【答案】（1）；（2）1；（3）.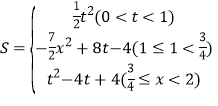

【解析】

①由题目意思可知△MNQ和△ABC为等腰直角三角形，又MN⊥AB，可知MB=MN=AB-AM,可得答案.②此时MN=AM=BM,M为AB的中点，由长度除以速度即可得出时间t.③M不与A,B重合，有分析知道MN在AB中点前 面积S=×时达到最小；之后面积逐渐减小.

①MN=AB-AM=,②t=S=×

当N与C重合时，设QN与AC交于D,QM与AC交于E, S=S△MNQ-S△DQE=×（）2-（4-3t）2=；当N过BC中点后， S=×MN2=×（）2=.