题目内容
【题目】已知△ABC为等边三角形，BD为△ABC的高，延长BC至E，使CE=CD=1，连接DE，则BE=___________，∠BDE=_________ ．
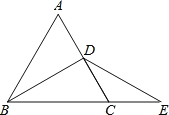
【答案】3 120°
【解析】
根据等腰三角形和30度角所对直角边等于斜边的一半，得到BC的长，进而得到BE的长，根据三角形外角性质求出∠E=∠CDE=30°，进而得出∠BDE的度数．
∵△ABC为等边三角形，∴∠ABC=∠ACB=60°，AB=BC．
∵BD为高线，∴∠BDC=90°，∠DBC
∠ABC=30°，
∴BC=2DC=2，∴BE=BC+CE=2+1=3．
∵CD=CE，∴∠E=∠CDE．
∵∠E+∠CDE=∠ACB=60°，∴∠E=∠CDE=30°，
∴∠BDE=∠BDC+∠CDE=120°．
故答案为：3，120°．
【题目】初三学生小丽、小杰为了解本校初二学生每周上网的时间，各自在本校进行了抽样调查．小丽调查了初二电脑爱好者中
名学生每周上网的时间，算得这些学生平均每周上网时间为
小时；小杰从全体
名初二学生名单中随机抽取了名学生，调查了他们每周上网的时间，算得这些学生平均每周上网时间为
小时．小丽与小杰整理各自样本数据，如下表所示．
时间段（小时/周） | 小丽抽样人数 | 小杰抽样人数 |
|
|
|
|
|
|
|
|
|
|
|
|
（每组可含最低值，不含最高值）
请根据上述信息，回答下列问题：
你认为哪位学生抽取的样本具有代表性？答：________；估计该校全体初二学生平均每周上网时间为________小时；
根据具有代表性的样本，把上图中的频数分布直方图补画完整；
在具有代表性的样本中，中位数所在的时间段是________小时/周；
专家建议每周上网
小时以上（含小时）的同学应适当减少上网的时间，根据具有代表性的样本估计，该校全体初二学生中有多少名同学应适当减少上网的时间？
