题目内容
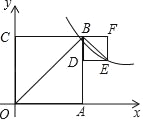
【题目】点A、B分别在x轴负半轴和y轴正半轴上,点C(2,-2),CA、CB分别交坐标轴于D、E,CA⊥AB,且CA=AB.

(1)求点B的坐标;
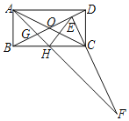
(2)如图2,连接DE,求证:BD-AE=DE.
【答案】(1)B(0,4);(2)见解析
【解析】
(1)作CM⊥x轴于M,求出CM=OM=2,利用AAS证出△BAO≌△ACM,得出AO=CM=2,OB=AM=4,即可得出答案;
(2)在BD上截取BF=AE,连AF,证△BAF≌△CAE,证△AFD≌△CED,即可得出答案.
解:(1)如图1,作CM⊥x轴于M,

∵C(2,-2),
∴CM=2,OM=2,
∵AB⊥AC,
∴∠BAC=∠AOB=∠CMA=90°,
∴∠BAO+∠CAM=90°,∠CAM+∠ACM=90°,
∴∠BAO=∠ACM,
在△BAO和△ACM中

∴△BAO≌△ACM,
∴AO=CM=2,OB=AM=AO+OM=2+2=4,
∴B(0,4).
(2)证明:如图2,在BD上截取BF=AE,连AF,

∵△BAO≌△CAM,
∴∠ABF=∠CAE,
在△ABF和△ACE中,

∴△ABF≌△CAE(SAS),
∴AF=CE,∠ACE=∠BAF=45°,
∵∠BAC=90°,
∴∠FAD=45°=∠ECD,
由(1)可知OA=OM,OD∥CM,
∴AD=DC,(图1中),
在△AFD和△CED中,

∴△AFD≌△CED(SAS),
∴DE=DF,
∴BD-AE=DE;

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目