题目内容
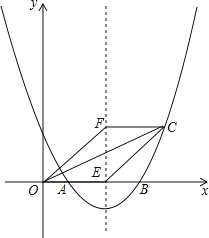
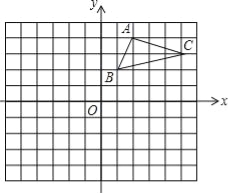
【题目】已知如图,边长为2的正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
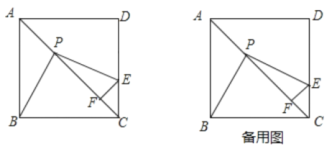
(1)求证:![]() :
:
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
(3)在点![]() 的运动过程中,
的运动过程中,![]() 能否为等腰三角形?如果能,直接写出此时
能否为等腰三角形?如果能,直接写出此时![]() 的长;如果不能,试说明理由.
的长;如果不能,试说明理由.
【答案】(1)见解析;(2)![]() 的长度不变,值为
的长度不变,值为![]() ,见解析;(3)能,
,见解析;(3)能,![]() 的长为2.
的长为2.
【解析】
(1)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,根据正方形的性质证明
,根据正方形的性质证明![]() ,即可求解;
,即可求解;
(2)连接![]() ,证明
,证明![]() ,得到
,得到![]() ;
;
(3)根据题意分①若点![]() 在线段
在线段![]() 上②若点
上②若点![]() 在线段
在线段![]() 的延长线上,分别求解即可.
的延长线上,分别求解即可.
解:(1)证明:过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,如图1.
,如图1.
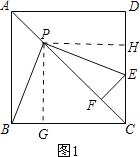
∵四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() 即
即![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
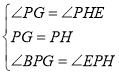 .
.
∴![]() ,
,
∴![]() .
.
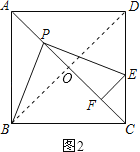
(2)连接![]() ,如图2.
,如图2.
∵四边形![]() 是正方形,∴
是正方形,∴![]() .
.
∵![]() 即
即![]() ,
,
∴![]() .
.
∵![]() 即
即![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() .
.
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴点![]() 在运动过程中,
在运动过程中,![]() 的长度不变,值为
的长度不变,值为![]() .
.
(3)![]() 的长为2.
的长为2.
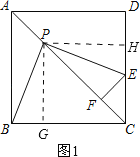
①若点![]() 在线段
在线段![]() 上,如图1.
上,如图1.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
若![]() 为等腰三角形,则
为等腰三角形,则![]() .
.
∴![]() ,
,
∴![]() ,与
,与![]() 矛盾,
矛盾,
∴当点![]() 在线段
在线段![]() 上时,
上时,![]() 不可能是等腰三角形.
不可能是等腰三角形.
②若点![]() 在线段
在线段![]() 的延长线上,如图4.
的延长线上,如图4.

若![]() 是等腰三角形,
是等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() 的长为2.
的长为2.

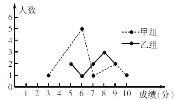
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.