题目内容
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
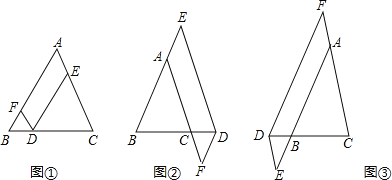
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
【答案】解:(1)证明:∵DF∥AC,DE∥AB,∴四边形AFDE是平行四边形。∴AF=DE。
∵DF∥AC,∴∠FDB=∠C。
又∵AB=AC,∴∠B=∠C。∴∠FDB=∠C。∴DF=BF。∴DE+DF=AB=AC。
(2)图②中:AC+DF=DE;图③中:AC+DE=DF。
(3)2或10。
【解析】
试题(1)证明四边形AFDE是平行四边形,且△DEC和△BDF是等腰三角形即可证得。
(2)与(1)的证明方法相同。
(3)根据(1)(2)中的结论直接求解:
当如图①的情况,DF=AC﹣DE=6﹣4=2;
当如图③的情况,DF=AC+DE=6+4=10。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】今年十一黄金周期间,九寨沟7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化/万人 | +0.5 | +0.7 | +0.8 |
|
| +0.2 |
|
(1)、请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?(5分)
(2)、如果9月30日旅游人数为2.5万人,平均每人消费500元,请问风景区在此7天内总收入为多少万元?