题目内容
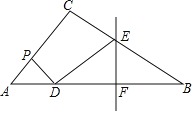
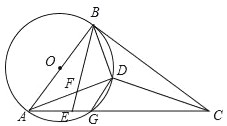
【题目】如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
(1)求证:BC是⊙O的切线;
(2)求证:DF=DG;
(3)若∠ADG=45°,DF=1,则有两个结论:①ADBD的值不变;②AD-BD的值不变,其中有且只有一个结论正确,请选择正确的结论,证明并求其值.
【答案】(1)证明见解析;(2)证明见解析;(3)正确的结论:AD﹣BD的值不变,证明见解析,AD﹣BD=![]() .
.
【解析】试题分析:(1)根据三角形内心的性质得出∠DBC=∠DBE,进而根据已知求得∠DBC=∠BAD,根据圆周角定理即可证得![]() 从而求得AB⊥BC,证得结论;
从而求得AB⊥BC,证得结论;
(2)连接![]() ,根据圆内接四边形外角的性质得出
,根据圆内接四边形外角的性质得出![]() 由三角形外角的性质求得
由三角形外角的性质求得![]() 证得
证得![]() 进而求得
进而求得![]() 由三角形内心的性质得出
由三角形内心的性质得出![]() 然后根据AAS证得△DEF≌△DEG,从而证得
然后根据AAS证得△DEF≌△DEG,从而证得![]()
(3)在AD上截取DH=BD,连接BH、BG,证得![]() 是等腰直角三角形,得出
是等腰直角三角形,得出![]() 然后证得△ABH∽△GBD,得出
然后证得△ABH∽△GBD,得出![]() 求得
求得![]() 即可求得
即可求得![]()
试题解析:(1)证明:∵D为△BCE内心,
∴∠DBC=∠DBE,
∵∠DBE=∠BAD.
∴∠DBC=∠BAD,
∵AB是![]() 的直径,
的直径,
∴![]()
∴![]()
∴![]()
即![]()
∴AB⊥BC,
∴BC是![]() 的切线;
的切线;
(2)证明:如图1,连接DE,
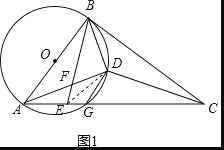
∵∠DBC=∠BAD,∠DBC=∠DBE,
∴∠DBE=∠BAD,
∴∠ABF+∠BAD=∠ABF+∠DBE,
∴∠BFD=∠ABD,
∵∠DGC=∠ABD,
∴∠BFD=∠DGC,
∴∠DFE=∠DGE,
∵D为△BCE内心,
∴∠DEG=∠DEB,
在△DEF和△DEG中
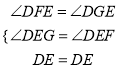 ,
,
∴△DEF≌△DEG(AAS),
∴DF=DG;
(3)ADBD的值不变;
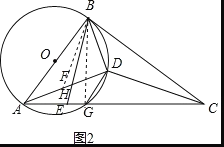
如图2,在AD上截取DH=BD,连接BH、BG,
∵AB是直径,
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴∠AHB=∠BDG,
∵∠BAD=∠BGD,
∴△ABH∽△GBD,
∴![]()
∵DG=1,
∴![]()
∵ADBD=ADDH=AH,
∴![]()