Question

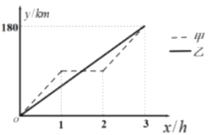
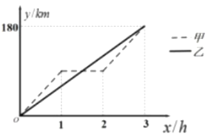
【题目】甲、乙两车间同时从A地出发前往B地，沿着相同的路线匀速驶向B地，甲车中途由于某种原因休息了1小时，然后按原速继续前往B地，两车离A地的距离y(km)与行驶的时间x(h)之间的函数关系如图所示：

(1)A、B两地的距离是__________km；

(2)求甲车休息后离A地的距离y(km)与x(h)之间的函数关系；

(3)请直接写出甲、乙两车何时相聚15km。

Answer 1

【答案】（1）180；（2）；（3）甲乙两车出发0.5h或1.25h或1.75h或2.5h时两车距离15km

【解析】

(1)根据图象解答即可;(2) 根据函数图象中的数据可以求得甲车再次行驶过程中y与x之间的函数关系式；(3) 根据题意，利用分类讨论的数学思想可以求得x的值．

解：

(1)观察图象可得：A、B两地的距离是180km;

(2)由题意得，甲车的平均速度为：180÷(3-1)=90

所以当x=1时，y=90

当x=2时，y=90

当2≤x≤3时，设(k≠0)

点(2，90)，(3，180)在直线上

因此有

解得：

∴

∴甲车休息后离A地的距离为y(km)与x(h)之间的函数关系为：

(3) 设乙车行驶过程中y与x之间的函数关系式是y=ax，
180=3a，得a=60，
∴乙车行驶过程中y与x之间的函数关系式是y=60x，

∴60x=90,得x=1.5,即两车1.5小时相遇，

当0≤x≤1.5时，甲车行驶过程中y与x之间的函数关系式是y=90x，90=x,
∴90x-60x=15，得x=，
90-60x=15时，x=1.25，

当1.5≤x≤3时，甲车行驶过程中y与x之间的函数关系式是y=9x-90，
90=x，
∴60x-90=1.5,得x=1.75;

60x-(90x-90)=15,得x=2.5

由上可得，甲乙两车出发0.5h或1.25h或1.75h或2.5h时两车距离15km。