Question

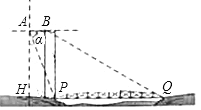
【题目】如图，在△ABC中，AD⊥BC于点D，点F为AB上一点，连接CF，过点B作BE⊥BC交CF的延长线于点E，交AD于点H，且∠1=∠2

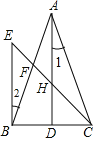
（1）求证：AB=AC；

（2）若∠1=22°，∠AFC=110°，求∠BCE的度数．

Answer 1

【答案】（1）见解析；（2）42°

【解析】

（1）先证明∠ABC=∠ACB，再根据等角对等边得出结论．

（2）先求出∠FBC，再根据∠AFC=∠FBC+∠ECB求解．

（1）证明：∵EB⊥BC，AD⊥BC，

∴EB∥AD，

∴∠2=∠BAD，

∵∠1=∠2，

∴∠BAD=∠1，

∵∠1+∠ACD=90°，∠BAD+∠ABC=90°，

∴∠ABC=∠ACB，

∴AB=AC．

（2）解：∵∠2=∠1=22°，∠EBC=90°，

∴∠FBC=68°，

∵∠AFC=∠FBC+∠ECB，

∴∠ECB=110°-68°=42°．