Question

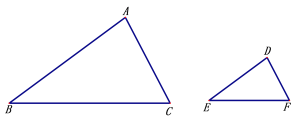
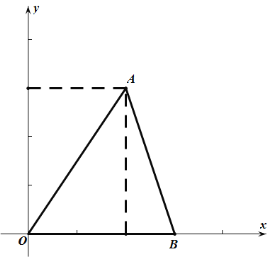
【题目】如图1，在ABCD中，∠D=45°，E为BC上一点，连接AC，AE，

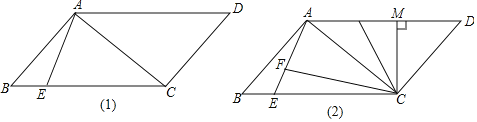
（1）若AB=2，AE=4，求BE的长；

（2）如图2，过C作CM⊥AD于M，F为AE上一点，CA=CF，且∠ACF=∠BAE，求证：AF+AB=AM．

Answer 1

【答案】（1）2-2；（2）见解析

【解析】

（1）如图（1），过A作AH⊥BC于H，解直角三角形即可得到结论；

（2）如图（2），在AM上截取MN=MC，在△ACF内以AF为底边作等腰直角三角形AFP，连接CP，根据平行线的性质函数三角形的内角和得到∠CAN=∠PAC，求得∠APC=∠FPC==135°=∠ANC，根据全等三角形的性质得到AP=AN，于是得到结论．

解：（1）如图（1），过A作AH⊥BC于H，

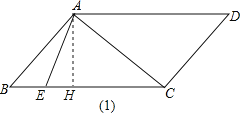
在ABCD中，∠D=∠B=45°，AB=2，

∴AH=BH=2，

∵AE=4，

∴EH==2，

∴BE=BH-EH=2-2；

（2）如图（2），在AM上截取MN=MC，在△ACF内以AF为底边作等腰直角三角形AFP，连接CP，

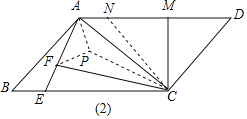
∵∠AFC+∠FAC+∠ACF=180°，∠B+∠FAC+∠BAF+∠CAN=180°，

∴∠AFC=∠B+∠CAN=45°+∠CAN，

∵∠FAC=∠FAP+∠PAC=45°+∠PAC，∴∠FAC=∠∠AFC，

∴∠CAN=∠PAC，

∵∠APC=∠FPC==135°=∠ANC，

∴△APC≌△ANC（AAS），

∴AP=AN，

∵AM=AN+MN，

∴AM=AN+MN=AF+CD=AF+AB，

即AF+AB=AM．