Question

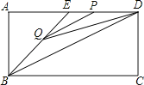
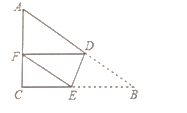
【题目】如图，△ABC中，∠C=90°，D、E是AB、BC上两点，将△ABC沿DE折叠，使点B落在AC边上点F处，并且DF∥BC，若CF=3，BC=9，则AB的长是( )

A. B. 15C. D. 9

Answer 1

【答案】C

【解析】

由折叠得到EB=EF，∠B=∠DFE，根据CE+EB=9，得到CE+EF=9，设EF=x，得到CE=9-x，在直角三角形CEF中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出EF与CE的长，由FD与BC平行，得到一对内错角相等，等量代换得到一对同位角相等，进而确定出EF与AB平行，由平行得比例，即可求出AB的长．

由折叠得到EB=EF，∠B=∠DFE，

在Rt△ECF中，设EF=EB=x，得到CE=BC-EB=9-x，

根据勾股定理得：EF2=FC2+EC2，即x2=32+（9-x）2，

解得：x=5，

∴EF=EB=5，CE=4，

∵FD∥BC，

∴∠DFE=∠FEC，

∴∠FEC=∠B，

∴EF∥AB，

∴，

则AB===，

故选：C．