题目内容
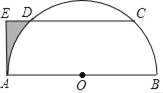
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD//BM,交AB于点F,且![]() ,连接AC,AD,延长AD交BM于点E.
,连接AC,AD,延长AD交BM于点E.
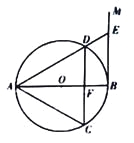
(l)求证:△ACD是等边三角形;
(2)连接OE,若DE=2,求OE的长.
【答案】(1)见解析(2)![]()
【解析】试题(1)根据切线的定义可知AB⊥BM,又∵BM//CD,∴AB⊥CD,根据圆的对称性可得AD=AC,再根据等弧对等弦得DA=DC,即DA=DC=AC,所以可得△ACD是等边三角形;(2)△ACD为等边三角形,AB⊥CD,由三线合一可得∠DAB=30°,连接BD,根据直径所对的角是直角和三角形的内角和可得∠∠EBD=∠DAB=30°,因为DE=2,求出BE=4,根据勾股定理得![]() ,直角三角形中30°角所对的直角边等于斜边的一半得,
,直角三角形中30°角所对的直角边等于斜边的一半得, ![]() ,
, ![]() ,在Rt△OBE中,根据勾股定理即可得出OE的长.
,在Rt△OBE中,根据勾股定理即可得出OE的长.
试题解析:证:∵BM是⊙O切线,AB为⊙O直径,∴AB⊥BM,∵BM//CD,∴AB⊥CD,
∴AD=AC,∴AD=AC,∴DA=DC,∴DC=AD,∴AD=CD=AC,∴△ACD为等边三角形.
证:(2)△ACD为等边三角形,AB⊥CD,∴∠DAB=30°,连结BD,∴BD⊥AD.
∠EBD=∠DAB=30°,∵DE=2,∴BE=4, ![]() ,
, ![]() ,
, ![]() ,
,
在Rt△OBE中, ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某产品每件成本10元,试销阶段每件产品的销售价![]() (元)与产品日销售量
(元)与产品日销售量![]() (元)间的关系如下:
(元)间的关系如下:
| … | 12 | 15 | 18 | 21 | 24 | … |
| … | 28 | 25 | 22 | 19 | 16 | … |
日销售量![]() 是销售价
是销售价![]() 的一次函数.
的一次函数.
(1)求出日销售量![]() (件)与销售量
(件)与销售量![]() (元)的函数关系式.
(元)的函数关系式.
(2)要使每日的销售利润200元,每件产品的销售应定为多少元?进货成本多少元?
(3)选作:要使每日的销售的利润最大,每件产品的销售价应定为多少元?