题目内容
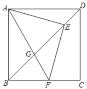
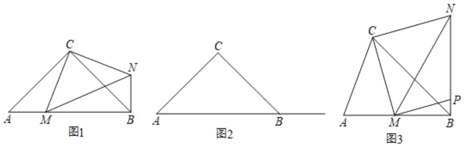
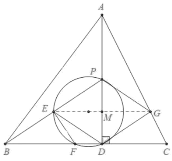
【题目】如图,在ABC中,已知AB=BC=10,AC=4![]() ,AD为边BC上的高线,P为边AD上一点,连结BP,E为线段BP上一点,过D、P、E三点的圆交边BC于F,连结EF.
,AD为边BC上的高线,P为边AD上一点,连结BP,E为线段BP上一点,过D、P、E三点的圆交边BC于F,连结EF.
(1)求AD的长;
(2)求证:△BEF∽△BDP;
(3)连结DE,若DP=3,当△DEP为等腰三角形时,求BF的长;
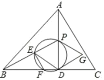
(4)把△DEP沿着直线DP翻折得到△DGP,若G落在边AC上,且DG∥BP,记△APG、△PDG、△GDC的面积分别为S1、S2、S3,则S1:S2:S3的值为 .
【答案】(1)AD=8,见解析;(2)△BEF∽△BDP,见解析;(3)BF的长为![]() 、
、![]() 、
、![]() ,见解析;(4)S1:S2:S3=3:3:2,见解析.
,见解析;(4)S1:S2:S3=3:3:2,见解析.
【解析】
(1)设CD=x,则BD=10-x,在Rt△ABD和Rt△ACD中利用勾股定理列方程即可求出x,进而求出AD,
(2)由圆内接四边形性质可知∠BFE=∠BPD,即可证明△BEF∽△BDP
(3)因为DP=3,由②BP=3![]() ,可得分三种情况PE=DP、DE=PE、DP=DE利用直角三角形和等腰三角形性质先求出EB,再根据
,可得分三种情况PE=DP、DE=PE、DP=DE利用直角三角形和等腰三角形性质先求出EB,再根据![]() 即可求解;
即可求解;
(4)连接EG交PD于M点,DG∥BP和折叠的性质可得∠EPD=∠EDF=∠PDG,EP=PG=ED=DG,即可得出E是BP中点,进而求出![]() ,由
,由![]() ,即可求出PM=2,PD=4,AP=4,再利用三角形面积求法即可解答.
,即可求出PM=2,PD=4,AP=4,再利用三角形面积求法即可解答.
解:(1)设CD=x,则BD=10﹣x,
在Rt△ABD和Rt△ACD中,AD2=AB2﹣BD2=AC2﹣CD2,
依题意得:![]() ,
,
解得x=6,
∴AD=![]() =8.
=8.
(2)∵四边形BFEP是圆内接四边形,
∴∠EFB=∠DPB,
又∵∠FBE=∠PDB,
∴△BEF∽△BDP.
(3)由(1)得BD=6,
∵PD=3,
∴BP=![]() =
=![]() ,
,
∴cos∠PBD=![]() ,
,
当△DEP为等腰三角形时,有三种情况:
Ⅰ.当PE=DP=3 时,BE=BP﹣EP=![]() ,
,
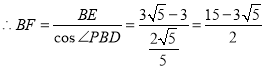
Ⅱ.当DE=PE时,E是BP中点,BE=![]() ,
,
![]()
Ⅲ.当DP=DE=3时,PE=2×PDcos∠BPD=![]() =
=![]() ,
,
![]()
![]()
若DP=3,当△DEP为等腰三角形时,BF的长为![]() 、
、![]() 、
、![]() .
.
(4)连接EG交PD于M点,
∵DG∥BP
∴∠EPD=∠EDF=∠PDG,
∴PG=DG,
∵EP=PG,ED=DG,
∴四边形PEDG是菱形,
∴EM=MG,PM=DM,EG⊥AD,
又∵BD⊥AD,
∴EG∥BC,
∴EM=![]() BD=3=MG,,
BD=3=MG,,
∴![]() ,
,
∴AM=6,
∴DM=PM=2,
∴PD=4,AP=4,
∴S△APG=![]() =
=![]() ×4×3=6,
×4×3=6,
S△PDG=![]() =
=![]() ×4×3=6,
×4×3=6,
S△GDC=![]() =
=![]() =4.
=4.
∴S1:S2:S3=6:6:2=3:3:2.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案