题目内容
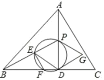
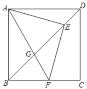
【题目】如图,在正方形ABCD中,AB=3,点E是对角线BD上的一点,连结AE,过点E作EF垂直AE交BC于点F,连结AF,交对角线BD于G.若三角形AED与四边形DEFC的面积之比为3:8,则cos∠GEF=_____.
【答案】![]()
【解析】
连接CE,作EH⊥CD于H,EM⊥BC于M,则四边形EMCH是矩形,得出EM=CH,CM=EH,由正方形的性质得出BC=CD=3,∠ABC=90°,AB=CB,∠ABE=∠CBE=∠BDC=45°,证明△ABE≌△CBE得出EA=EF,∠BAE=∠BCE,同理:△ADE≌△CDE,得出△ADE的面积=△CDE的面积,由已知得出△CDE:△CEF的面积=3:5,证明A、B、F、E四点共圆,由圆周角定理得出∠GEF=∠BAF,∠EFC=∠BAE=∠BCE,得出EF=EC,由等腰三角形的性质得出FM=CM=EH=DH,设FM=CM=EH=DH=x,则FC=2x,EM=HC=3-x,由△CDE:△CEF的面积=3:5得出方程,解得:x=![]() ,得出FC=1,BF=BC-FC=2,由勾股定理求出AF=
,得出FC=1,BF=BC-FC=2,由勾股定理求出AF=![]() ,即可得出结果.
,即可得出结果.
解:连接CE,作EH⊥CD于H,EM⊥BC于M,如图所示:
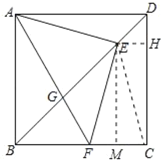
则四边形EMCH是矩形,
∴EM=CH,CM=EH,
∵四边形ABCD是正方形,
∴BC=CD=3,∠ABC=90°,AB=CB,∠ABE=∠CBE=∠BDC=45°,
在△ABE和△CBE中,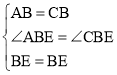 ,
,
∴△ABE≌△CBE(SAS),
∴EA=EF,∠BAE=∠BCE,
同理:△ADE≌△CDE,
∴△ADE的面积=△CDE的面积,
∵△AED与四边形DEFC的面积之比为3:8,
∴△CDE:△CEF的面积=3:5,
∵EF⊥AE,
∴∠AEF=90°,
∴∠ABC+∠AEF=180°,
∴A、B、F、E四点共圆,
∴∠GEF=∠BAF,∠EFC=∠BAE=∠BCE,
∴EF=EC,
∵EM⊥BC,
∴FM=CM=EH=DH,
设FM=CM=EH=DH=x,则FC=2x,EM=HC=3﹣x,
∵△CDE:△CEF的面积=3:5,
∴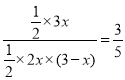 ,
,
解得:x=![]() ,
,
∴FC=1,BF=BC﹣FC=2,
∴AF=![]() ,
,
∴cos∠GEF=cos∠BAF=![]() =
=![]() =
=![]() ;
;
故答案为:![]() .
.