题目内容
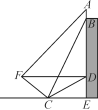
【题目】如图,光明中学一教学楼顶上竖有一块高为AB的宣传牌,点E和点D分别是教学楼底部和外墙上的一点(A,B,D,E在同一直线上),小红同学在距E点9米的C处测得宣传牌底部点B的仰角为67°,同时测得教学楼外墙外点D的仰角为30°,从点C沿坡度为1∶![]() 的斜坡向上走到点F时,DF正好与水平线CE平行.
的斜坡向上走到点F时,DF正好与水平线CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若在点F处测得宣传牌顶部A的仰角为45°,求出宣传牌AB的高度(结果精确到0.01).(注:sin67°≈0.92,tan67°≈2.36,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】(1) 3![]() 米 (2) 1.95米
米 (2) 1.95米
【解析】
(1)利用正切函数定义解三角形求DE长度.(2)利用坡度定义,解直角三角形.
解:(1)过点F作FH⊥CE于H.∵FH∥DE,DF∥HE,∠FHE=90°,∴四边形FHED是矩形,则FH=DE,在Rt△CDE中,DE=CE·tan∠DCE=9×tan30°=3![]() (米),∴FH=DE=3
(米),∴FH=DE=3![]() (米).答:点F到CE的距离为3
(米).答:点F到CE的距离为3![]() 米
米
(2)∵CF的坡度为1∶![]() ,∴在Rt△FCH中,CH=
,∴在Rt△FCH中,CH=![]() FH=9(米),∴EH=DF=18(米),在Rt△BCE中,BE=CE·tan∠BCE=9×tan67°≈21.24(米),∴AB=AD+DE-BE=18+3
FH=9(米),∴EH=DF=18(米),在Rt△BCE中,BE=CE·tan∠BCE=9×tan67°≈21.24(米),∴AB=AD+DE-BE=18+3![]() -21.24≈1.95(米)
-21.24≈1.95(米)
答:宣传牌AB的高度约为1.95米

【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?