Question

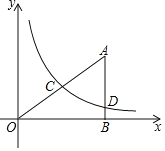
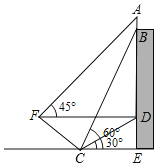
【题目】为积极参与文明城市创建活动，我市某校在教学楼顶部新建了一块大型宣传牌，如下图。小明同学为测量宣传牌的高度AB，他站在距离教学楼底部E处6米远的地面C处，测得宣传牌的底部B的仰角为60°，同时测得教学楼窗户D处的仰角为30°（A、B、D、E在同一直线上）。然后，小明沿坡度i=1：1.5的斜坡从C走到F处，此时DF正好与地面CE平行。

（1）求点F到直线CE的距离（结果保留根号）；

（2）若小明在F处又测得宣传牌顶部A的仰角为45°，求宣传牌的高度AB（结果精确到0.1米，）。

Answer 1

【答案】（1）点F到地面的距离为米；（2）宣传牌的高度约为4.3米

【解析】

（1））过点F作FG⊥EC于G,先证得FG=DE，再根据tan∠30°求出DE的长即可得到答案；

（2）根据CF为坡度i=1：1.5的斜坡，求出CG的长，由此得到DF，再利用tan45°

解：（1）过点F作FG⊥EC于G

依题意知FG∥DE，DF∥GE，∠FGE=90°

∴四边形DEGF是矩形；

∴FG=DE，

在Rt△CDE中，

DE=CEtan∠DCE=6tan∠30°=(米）

∴点F到地面的距离为米

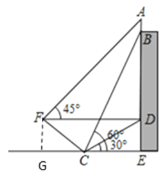
（2）∵斜坡CF的坡度为i=1:1.5，

∴Rt△CFG中，CG=1.5 FG=×1.5=，

∴FD=EG=+6，

在Rt△ADF中，

，

在Rt△BCE中，

BE=CEtan∠BCE=6tan∠60°=，

∴AB=AD+DE-BE

=+6+-=6- 4.3(米）

答：宣传牌的高度约为4.3米