题目内容
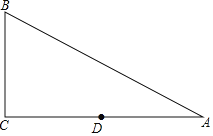
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是边AC的中点,点E,F在边AB上,当△DEF是等腰三角形,且底角的正切值是![]() 时,△DEF腰长的值是_____.
时,△DEF腰长的值是_____.
【答案】![]() 或
或![]()
【解析】
由勾股定理得出AB=![]() =5,作DM⊥AB于M,由三角函数得出DM=
=5,作DM⊥AB于M,由三角函数得出DM=![]() ,分三种情况:①当DE=DF时,②当ED=EF时,作EN⊥DF于N,③当FE=FD时,作FG⊥DE于G;由等腰三角形的性质、三角函数定义和勾股定理即可得出答案.
,分三种情况:①当DE=DF时,②当ED=EF时,作EN⊥DF于N,③当FE=FD时,作FG⊥DE于G;由等腰三角形的性质、三角函数定义和勾股定理即可得出答案.
∵∠C=90°,AC=4,BC=3,
∴AB=![]() =5,
=5,
∵点D是边AC的中点,
∴AD=![]() AC=2,作DM⊥AB于M,如图1所示:
AC=2,作DM⊥AB于M,如图1所示:
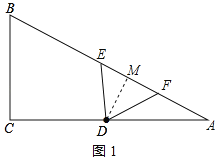
∵sinA=![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴DM=![]() ,
,
分三种情况:
①当DE=DF时,
∵tan∠DFE=![]() =
=![]() ,
,
∴FM=![]() DM=
DM=![]() ×
×![]() =
=![]() ,
,
∴DE=DF=![]() =
=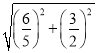 =
=![]() ;
;
②当ED=EF时,作EN⊥DF于N,如图2所示:
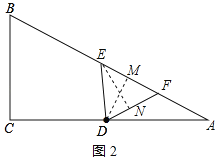
由①得:DM=![]() ,FM=
,FM=![]() ,DF=
,DF=![]() ;
;
∵EN⊥DF,∴FN=DN=![]() DF=
DF=![]() ,
,
∵tan∠EFD=![]() =
=![]() ,
,
∴EN=![]() FN=
FN=![]() ,
,
∴ED=EF=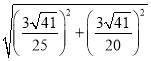 =
=![]() ;
;
③当FE=FD时,作FG⊥DE于G,如图3所示:
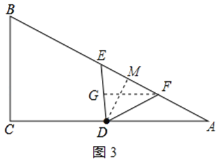
则EG=DG,
同①得:EM=![]() ,DE=
,DE=![]() ,
,
∴EG=![]() ,
,
∵tan∠DEF=![]() =
=![]() ,
,
∴GF=![]() EG=
EG=![]() ,
,
∴EF=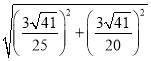 =
=![]() ;
;
综上所述,当△DEF是等腰三角形,且底角的正切值是![]() 时,△DEF腰长的值是
时,△DEF腰长的值是![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目