题目内容
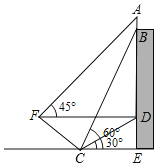
【题目】如图，小明利用所学数学知识测量某建筑物BC高度，采用了如下的方法：小明从与某建筑物底端B在同一水平线上的A点出发，先沿斜坡AD行走260米至坡顶D处，再从D处沿水平方向继续前行若干米后至点E处，在E点测得该建筑物顶端C的仰角为72°，建筑物底端B的俯角为63°，其中点A、B、C、D、E在同一平面内，斜坡AD的坡度i=1：2.4，根据小明的测量数据，计算得出建筑物BC的高度约为（ ）米（计算结果精DE确到0.1米，参考数据：sin72°≈0.95，tan72°≈3.08，sin63°≈0.89，tan63°≈1.96）
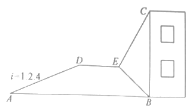
A.157.1 B.157.4 C.257.4 D.257.1
【答案】D
【解析】
如图作DH⊥AB于H，延长DE交BC于F．则四边形DHBF是矩形，在Rt△ADH中求出DH，再在Rt△EFB中求出EF，在Rt△EFC中求出CF即可解决问题
如图作DH⊥AB于H，延长DE交BC于F．
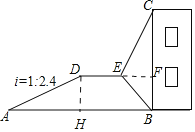
在Rt△ADH中，∵AD=260，DH：AH=1：2.4，
∴DH=100（m），
∵四边形DHBF是矩形，
∴BF=DH=100，
在Rt△EFB中，tan63°=
，
∴EF=
，
在Rt△EFC中，FC=EFtan72°，
∴CF=
×3.08≈157.1，
∴BC=BF+CF=257.1（m）．
故选D．
练习册系列答案
全优点练单元计划系列答案
相关题目
