题目内容
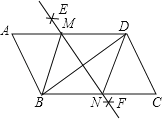
【题目】如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为________.
【答案】2![]()
【解析】
取AB与CD的中点M,N,连接MN,作点B关于MN的对称点E',连接E'C,E'B,此时CE的长就是GB+GC的最小值;先证明E点与E'点重合,再在Rt△EBC中,EB=2,BC=4,求EC的长.
取AB与CD的中点M,N,连接MN,作点B关于MN的对称点E′,连接E′C,E′B,
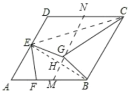
此时CE的长就是GB+GC的最小值;
∵MN∥AD,
∴HM=![]() AE,
AE,
∵HB⊥HM,AB=4,∠A=60°,
∴MB=2,∠HMB=60°,
∴HM=1,
∴AE′=2,
∴E点与E′点重合,
∵∠AEB=∠MHB=90°,
∴∠CBE=90°,
在Rt△EBC中,EB=2![]() ,BC=4,
,BC=4,
∴EC=![]() =2
=2![]() ,
,
故答案为2![]() .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目