题目内容
【题目】矩形ABCD中,AB=2,AD=4,将矩形ABCD绕点C顺时针旋转至矩形EGCF(其中E、G、F分别与A、B、D对应).
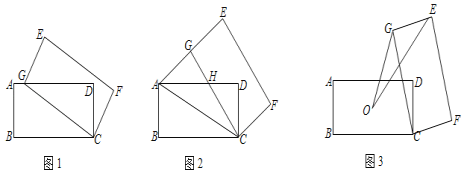
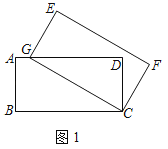
(1)如图1,当点G落在AD边上时,直接写出AG的长为 ;
(2)如图2,当点G落在线段AE上时,AD与CG交于点H,求GH的长;
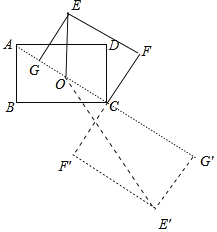
(3)如图3,记O为矩形ABCD对角线的交点,S为△OGE的面积,求S的取值范围.
【答案】(1)4﹣2![]() ;(2)
;(2)![]() ;(3)4﹣
;(3)4﹣![]() ≤S≤4+
≤S≤4+![]()
【解析】
(1)在Rt△DCG中,利用勾股定理求出DG即可解决问题;
(2)首先证明AH=CH,设AH=CH=m,则DH=AD﹣HD=4﹣m,在Rt△DHC中,根据CH2=CD2+DH2,构建方程求出m即可解决问题;
(3)如图,当点G在对角线AC上时,△OGE的面积最小,当点G在AC的延长线上时,△OE′G′的面积最大,分别求出面积的最小值,最大值即可解决问题.
解:(1)如图1中,
∵四边形ABCD是矩形,
∴BC=AD=CG=4,∠D=90°,
∵AB=CD=2,
∴DG=![]() =
=![]() =2
=2![]() ,
,
∴AG=AB﹣BG=4﹣2![]() ,
,
故答案为:4﹣2![]() .
.
(2)如图2中,
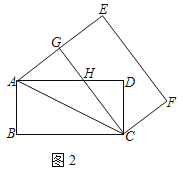
由四边形CGEF是矩形,得到∠CGE=90°,
∵点G在线段AE上,
∴∠AGC=90°,
∵CA=CA,CB=CG,
∴Rt△ACG≌Rt△ACB(HL).
∴∠ACB=∠ACG,
∵AB∥CD
∴∠ACG=∠DAC,
∴∠ACH=∠HAC,
∴AH=CH,设AH=CH=m,则DH=AD﹣AH=5﹣m,
在Rt△DHC中,∵CH2=DC2+DH2,
∴m2=22+(4﹣m)2,
∴m=![]() ,
,
∴AH=![]() ,GH=
,GH=![]() =
=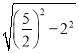 =
=![]() .
.
(3)在Rt△ABC中,![]() ,
,![]() ,
,
由题可知,G点在以C点为圆心,BC为半径的圆上运动,且GE与该圆相切,因为GE=AB不变,所以O到直线GE的距离即为△OGE的高,当点G在对角线AC上时,OG最短,即△OGE的面积最小,最小值=![]() ×OG×EG=
×OG×EG=![]() ×2×(4﹣
×2×(4﹣![]() )=4﹣
)=4﹣![]() .
.
当点G在AC的延长线上时,OG最长,即△OE′G′的面积最大.最大值=![]() ×E′G′×OG′=
×E′G′×OG′=![]() ×2×(4+
×2×(4+![]() )=4+
)=4+![]() .
.
综上所述,4﹣![]() ≤S≤4+
≤S≤4+![]() .
.