题目内容
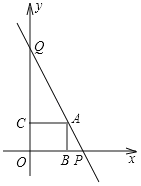
【题目】如图，在平面直角坐标系中，O为原点，点A在第一象限，点B是x轴正半轴上一点，∠OAB
45°，双曲线
过点A，交AB于点C，连接OC，若OC⊥AB，则tan∠ABO的值是_____．
【答案】
【解析】
过点C作CE垂直x轴，CD垂直AD，设点A的和点C的坐标，根据“AAS”证明△CEO≌△ADC，求出点A、C的坐标与k的关系，从而求出tan∠ABO的值.
作CE⊥x轴，AD⊥CD
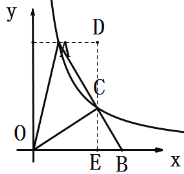
则∠D=∠OEC，∠ACD=∠COE
∵∠OAB
45°
∴AC=OC
∴△CEO≌△ADC
∴AD=CE,CD=OE
设AD=
,CD=b
可知点A的坐标为（
），点C的坐标为（
）
可得
∴
∴
∴
或
（舍），
∵∠ABO+∠BCE=∠BCE+∠OCE=90°，
∴∠ABO=∠OCE
∴tan∠ABO=tan∠OCE=
故答案是：
练习册系列答案
阅读快车系列答案
相关题目
