题目内容
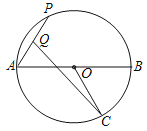
【题目】如图，AB是⊙O的直径，C为圆上一点，且∠AOC＝120°，⊙O的半径为2，P为圆上一动点，Q为AP的中点，则CQ的长的最值是_____．
【答案】1+
【解析】
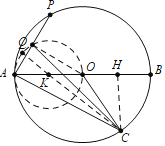
如图，连接OQ，作CH⊥AB于H．首先证明点Q的运动轨迹为以AO为直径的⊙K，连接CK，当点Q在CK的延长线上时，CQ的值最大，利用勾股定理求出CK即可解决问题.
解：如图，连接OQ，作CH⊥AB于H．
∵AQ＝QP，
∴OQ⊥PA，
∴∠AQO＝90°，
∴点Q的运动轨迹为以AO为直径的⊙K，连接CK，
当点Q在CK的延长线上时，CQ的值最大，
∵∠AOC＝120°，
∴∠COH＝60°，
在Rt△OCH中，
∵OC＝2，
∴OH＝
OC＝1，CH＝
，
在Rt△CKH中，CK＝
＝，
∴CQ的最大值为1+.
练习册系列答案
字词句段篇系列答案
相关题目
