题目内容
如图,Rt△ABO的顶点A是双曲线y= 与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
(1)y=﹣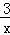 ,y=﹣x+2
,y=﹣x+2
(2)A为(﹣1,3),C为(3,﹣1),面积是4
解析试题分析:(1)欲求这两个函数的解析式,关键求k值.根据反比例函数性质,k绝对值为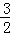 且为负数,由此即可求出k;
且为负数,由此即可求出k;
(2)交点A、C的坐标是方程组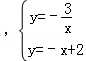 的解,解之即得;
的解,解之即得;
(3)从图形上可看出△AOC的面积为两小三角形面积之和,根据三角形的面积公式即可求出.
解:(1)设A点坐标为(x,y),且x<0,y>0,
则S△ABO= •|BO|•|BA|=
•|BO|•|BA|= •(﹣x)•y=
•(﹣x)•y=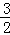 ,
,
∴xy=﹣3,
又∵y=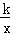 ,
,
即xy=k,
∴k=﹣3.
∴所求的两个函数的解析式分别为y=﹣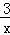 ,y=﹣x+2;
,y=﹣x+2;
(2)由y=﹣x+2,
令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2),
A、C两点坐标满足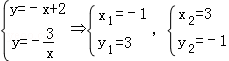
∴交点A为(﹣1,3),C为(3,﹣1),
∴S△AOC=S△ODA+S△ODC=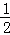 OD•(|x1|+|x2|)=
OD•(|x1|+|x2|)=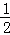 ×2×(3+1)=4.
×2×(3+1)=4.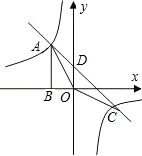
点评:此题首先利用待定系数法确定函数解析式,然后利用解方程组来确定图象的交点坐标,及利用坐标求出线段和图形的面积.

练习册系列答案
相关题目
为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )
| A.y=﹣2(x+1)2+2 | B.y=﹣2(x+1)2﹣2 |
| C.y=﹣2(x﹣1)2+2 | D.y=﹣2(x﹣1)2﹣2 |
 、
、 (单位:元)与正常运营时间
(单位:元)与正常运营时间 (单位:天)之间分别满足关系式:
(单位:天)之间分别满足关系式: 、
、 ,如图所示.
,如图所示.
 = 元,每辆车的改装费b= 元.正常运营 天后,就可以从节省燃料费中收回改装成本.
= 元,每辆车的改装费b= 元.正常运营 天后,就可以从节省燃料费中收回改装成本. .请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案?
.请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案?

 ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。