题目内容
如图1,正方形ABCD和正三角形EFG的边长都为1,点E,F分别在线段AB,AD上滑动,设点G到CD的距离为x,到BC的距离为y,记∠HEF为α(当点E,F分别与B,A重合时,记α=0°).(1)当α=0°时(如图2所示),求x,y的值(结果保留根号);
(2)当α为何值时,点G落在对角形AC上?请说出你的理由,并求出此时x,y的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| x | 0.03 | 0 | 0.29 | ||||
| y | 0.29 | 0.13 | 0.03 |
(参考数据:
| 3 |
| ||||
| 4 |
| ||||
| 4 |
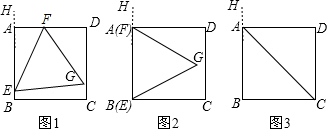
分析:(1)本题要依靠辅助线的帮助.过G作MN⊥AB于M交CD于N,GK⊥BC于K.求出MG,BM,求出x,y的值.
(2)过G作IQ∥BC交AB,CD于I,Q,过G作JP∥AB交AD,BC于J,P.证明Rt△GEI≌Rt△GFJ,推出∠AEF=∠AFE=45°.得出当α=45°时,点G在对角线AC上.已知∠AEG=105°,∠GEI=75°利用三角函数得出GI,GQ的值后得出x与y的关系.
(3)(4)是根据题意利用三角函数把α值代入可求解.
(2)过G作IQ∥BC交AB,CD于I,Q,过G作JP∥AB交AD,BC于J,P.证明Rt△GEI≌Rt△GFJ,推出∠AEF=∠AFE=45°.得出当α=45°时,点G在对角线AC上.已知∠AEG=105°,∠GEI=75°利用三角函数得出GI,GQ的值后得出x与y的关系.
(3)(4)是根据题意利用三角函数把α值代入可求解.
解答:解:(1)过G作MN⊥AB于M交CD于N,GK⊥BC于K.∵∠ABG=60°,BG=1,∴MG=
,BM=
.(2分)
∴x=1-
,y=
.(3分)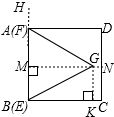
(2)当α=45°时,点G在对角线AC上,其理由是:(4分)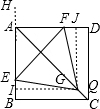
过G作IQ∥BC交AB,CD于I,Q,
过G作JP∥AB交AD,BC于J,P.
∵AC平分∠BCD,∴GP=GQ,∴GI=GJ.
∵GE=GF,
∴Rt△GEI≌Rt△GFJ,
∴∠GEI=∠GFJ.
∵∠GEF=∠GFE=60°,
∴∠AEF=∠AFE.
∵∠EAF=90°,
∴∠AEF=∠AFE=45度.
即α=45°时,点G落在对角线AC上.(6分)
(以下给出两种求x,y的解法)
方法一:
∵∠AEG=45°+60°=105°,
∴∠GEI=75度.
在Rt△GEI中,GI=GE•sin75°=
,
∴GQ=IQ-GI=1-
.(7分)
∴x=y=1-
.(8分)
方法二:当点G在对角线AC上时,有
+
+
x=
,(7分)
解得x=1-
∴x=y=1-
.(8分)
(3)
(10分)
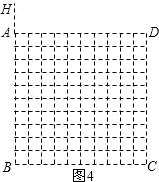
(4)由点G所得到的大致图形如图所示:
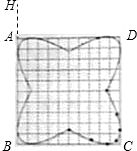 (12分)
(12分)
说明:1、第(2)问回答正确的得(1分),证明正确的得(2分),求出x,y的值各得(1分);
2、第(3)问表格数据,每填对其中4空得(1分);
3、第(4)问图形画得大致正确的得(2分),只画出图形一部分的得(1分).
| ||
| 2 |
| 1 |
| 2 |
∴x=1-
| ||
| 2 |
| 1 |
| 2 |

(2)当α=45°时,点G在对角线AC上,其理由是:(4分)

过G作IQ∥BC交AB,CD于I,Q,
过G作JP∥AB交AD,BC于J,P.
∵AC平分∠BCD,∴GP=GQ,∴GI=GJ.
∵GE=GF,
∴Rt△GEI≌Rt△GFJ,
∴∠GEI=∠GFJ.
∵∠GEF=∠GFE=60°,
∴∠AEF=∠AFE.
∵∠EAF=90°,
∴∠AEF=∠AFE=45度.
即α=45°时,点G落在对角线AC上.(6分)
(以下给出两种求x,y的解法)
方法一:
∵∠AEG=45°+60°=105°,
∴∠GEI=75度.
在Rt△GEI中,GI=GE•sin75°=
| ||||
| 4 |
∴GQ=IQ-GI=1-
| ||||
| 4 |
∴x=y=1-
| ||||
| 4 |
方法二:当点G在对角线AC上时,有
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
解得x=1-
| ||||
| 4 |
∴x=y=1-
| ||||
| 4 |
(3)
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| y | 0.13 | 0.03 | 0 | 0.03 | 0.13 | 0.29 | 0.50 |
| x | 0.50 | 0.29 | 0.13 | 0.03 | 0 | 0.03 | 0.13 |
(4)由点G所得到的大致图形如图所示:
 (12分)
(12分)说明:1、第(2)问回答正确的得(1分),证明正确的得(2分),求出x,y的值各得(1分);
2、第(3)问表格数据,每填对其中4空得(1分);
3、第(4)问图形画得大致正确的得(2分),只画出图形一部分的得(1分).
点评:点评:这是一道较好的压轴题,起点低,思路宽,一改那种“谈题色变”的面孔,而且又有较好的区分度.本题从表面看来是一个针对几何的相关知识进行考查的问题,但从试题的更深层次来理解,可以看到:在所有动态几何问题中,除去由于说理的需要而必须进行相关的合情推理论证及演绎推理外,更多的情况下还会遇到其运动变化过程中相关特殊位置的研究,而对这些特殊位置的研究常常是和几何问题的量化描述密不可分的,而其量化的描述一般会用到函数、方程或不等式.另外,还强化了对数形结合及用代数方法解决几何问题能力的考查.

练习册系列答案
相关题目
 21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上) (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )