题目内容
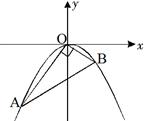
小明同学将直角三角板直角顶点置于平面直角坐标系的原点O,两直角边与抛物线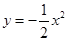 分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
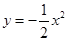 分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
(0,-2).
试题分析:设A(-m,-
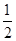 m2)(m>0),B(n,-
m2)(m>0),B(n,-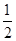 n2)(n>0),表示出直线AB解析式中b=-
n2)(n>0),表示出直线AB解析式中b=-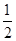 mn,再利用勾股定理得出mn=4,进而得出直线AB恒过其与y轴的交点C(0,-2).
mn,再利用勾股定理得出mn=4,进而得出直线AB恒过其与y轴的交点C(0,-2).设A(-m,-
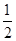 m2)(m>0),B(n,-
m2)(m>0),B(n,-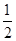 n2)(n>0),
n2)(n>0),设直线AB的解析式为:y=kx+b,则
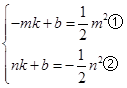
①×n+②×m得,(m+n)b=-
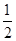 (m2n+mn2)=-
(m2n+mn2)=-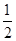 mn(m+n),
mn(m+n),∴b=-
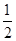 mn,
mn,由前可知,OB2=n2+
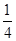 n4,OA2=m2+
n4,OA2=m2+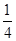 m4,AB2=(n+m)2+(-
m4,AB2=(n+m)2+(-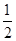 m2+
m2+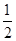 n2)2,
n2)2,由AB2=OA2+OB2,得:n2+
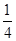 n4+m2+
n4+m2+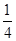 m4=(n+m)2+(-
m4=(n+m)2+(-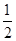 m2+
m2+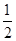 n2)2,
n2)2,化简,得mn=4.
∴b=-
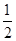 ×4=-2.由此可知不论k为何值,直线AB恒过点(0,-2),
×4=-2.由此可知不论k为何值,直线AB恒过点(0,-2),
练习册系列答案
相关题目
 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
 的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC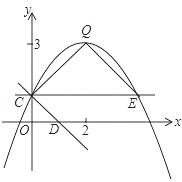
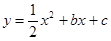 经过A(
经过A(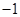 ,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.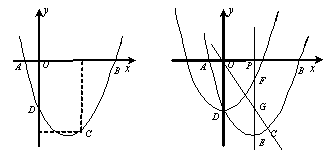
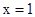 的抛物线的解析式 .
的抛物线的解析式 .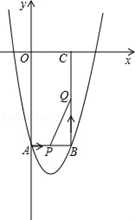


 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;