题目内容
已知抛物线 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
(1)求抛物线的解析式;
(2)若抛物线向下平移k个单位后经过点(-5,6)。
①求k的值及平移后抛物线所对应函数的最小值;
②设平移后抛物线与y轴交于点D,顶点为Q,点M是平移后的抛物线上的一个动点。请探究:当点M在何处时,△MBD的而积是△MPQ面积的2倍?求出此时点M的坐标。

 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。(1)求抛物线的解析式;
(2)若抛物线向下平移k个单位后经过点(-5,6)。
①求k的值及平移后抛物线所对应函数的最小值;
②设平移后抛物线与y轴交于点D,顶点为Q,点M是平移后的抛物线上的一个动点。请探究:当点M在何处时,△MBD的而积是△MPQ面积的2倍?求出此时点M的坐标。

(1)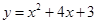 (2)①
(2)①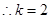 ∴对应函数的最小值是-3. ②∴点M的坐标是
∴对应函数的最小值是-3. ②∴点M的坐标是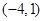 或
或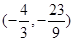
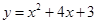 (2)①
(2)①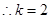 ∴对应函数的最小值是-3. ②∴点M的坐标是
∴对应函数的最小值是-3. ②∴点M的坐标是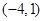 或
或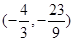
试题分析:(1)本题考查的是二次函数的性质以及待定系数法求二次函数解析式的相关知识,我们要注意根据已知条件选择合适的关系式的设法,本题利用一般式,把两点坐标代入关系式
 ,得到关于b、c的二元一次方程组,解方程组求出b、c的值,关系式便可得出.(2)若抛物线向下平移k个单位,
,得到关于b、c的二元一次方程组,解方程组求出b、c的值,关系式便可得出.(2)若抛物线向下平移k个单位,也就是y值减少k,求出对应的抛物线解析式,再利用公式求出最值.②画出图形分三种情况解答.
试题解析:(1)把(-1,0),(0,3)分别代入

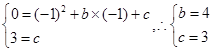
∴抛物线的解析式为
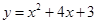
(2)①知平移后抛物线的解析式为
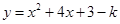
∵抛物线经过点(-5,6),
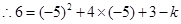 ;
;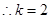
∴平移后抛物线的解析式为
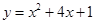
∴对应函数的最小值是-3
②由①知,BD=PQ=2,抛物线的对称轴为直线
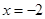 。
。又
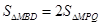
∴△MBD中BD边上的高是△MPQ中PQ边上的高的2倍。
设点M的坐标为
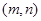 ,
,a.当点M在直线
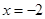 的左侧时,如图,则有
的左侧时,如图,则有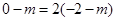 ,
,
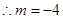 ,
,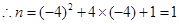 ,
,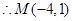 。
。 b.当点M在直线
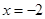 与y轴之间时,则有
与y轴之间时,则有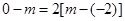
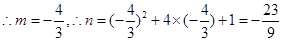 ,
,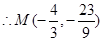
c.当点M在y轴右侧时,则有
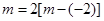
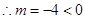 ,不合题意。
,不合题意。 ∴点M的坐标是
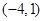 或
或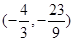

练习册系列答案
相关题目
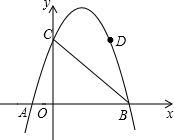

 的抛物线的解析式,y= .?
的抛物线的解析式,y= .?
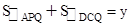 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.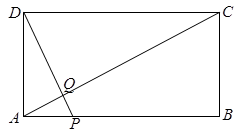
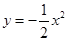 分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .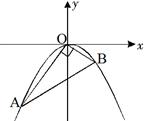
 ,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
 B.
B. C.
C. D.
D.