题目内容
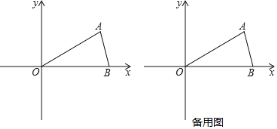
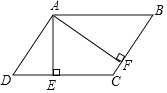
【题目】已知:如图,在△ABC中,∠ABC=45°,![]() ,AB=14,
,AB=14,
(1)求:△ABC的面积;
(2)若以C为圆心的圆C与直线AB相切,以A为圆心的圆A与圆C相切,试求圆A的半径.
【答案】(1)42;(2) 4或16
【解析】
(1)过C作CD⊥AB于D解直角三角形得到CD,根据三角形的面积公式即可得到结论;(2)根据圆C与直线AB相切,得到○C的半径,根据勾股定理得到AC,设○A的半径为r,当圆A与圆C内切时,当圆A与圆C外切时即可得到结论
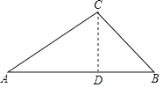
(1)过C作CD⊥AB于D,
∵![]() ,
,
∴![]() ,
,
∵∠ABC=45°,
∴BD=CD,
∵AB=14,
∴![]() ,
,
∴CD=6,
∴△ABC的面积![]() ;
;
(2)∵以C为圆心的圆C与直线AB相切,
∴⊙C的半径=6,
∵AD=8,
∴![]() ,
,
设⊙A的半径为r,
当圆A与圆C内切时,r﹣6=10,
∴r=16,
当圆A与圆C外切时,r+6=10,
∴r=4,
综上所述:以A为圆心的圆A与圆C相切,圆A的半径为:4或16.

练习册系列答案
相关题目