ЬтФПФкШн
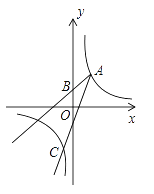
ЁОЬтФПЁПШчЭМЃЌA(2ЃЌ1)ЃЌB(2ЃЌ0)ЃЌCЮЊyжсЩЯвЛЖЏЕуЃЌЙ§AЃЌCСНЕуЕФХзЮяЯпЮЊЃКyЃНax2+bx+n(aЁй0ЃЌaЁйЉ1)ЃЌжБЯпOAгыжБЯпBCНЛгкЕуPЃЌ
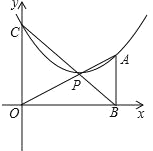
(1)ШєnЃН1ЃЌЧвХзЮяЯпЧЁКУвВЙ§PЕуЃЌжБНгаДГіХзЮяЯпЖЅЕузјБъЮЊЃК(_____ЃЌ______)
(2)ЕБХзЮяЯпЭЌЪБОЙ§AЃЌCЃЌPШ§ЕуЪБЃЌДЫЪБPБиЮЊИУХзЮяЯпЕФЖЅЕуЃЌЧывдnЃН2ЮЊР§бщжЄЩЯЪіНсТлЕФе§ШЗадЃЎ
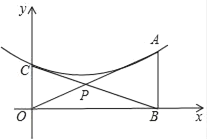
(3)ШєХзЮяЯпгыжБЯпBCгаЮЈвЛНЛЕуCЃЌ
ЂйЧѓaЕФжЕЃЛВЂЧѓЕБCбиyжсЯђЩЯдЫЖЏЪБЃЌЦфЖЅЕуЭЌЪБЯђЯТдЫЖЏЫљЖдгІnЕФШЁжЕЗЖЮЇЃЛ
ЂкЩшЙ§BСэгавЛжБЯп(гыBCЁЂABВЛжиКЯ)ЃЌвВгыХзЮяЯпНігавЛИіНЛЕуЃЌЩшЮЊDЃЌОЬНОПЗЂЯжЃКЮоТлCдкyжсЩЯШчКЮдЫЖЏЃЌжБЯпCDвЛЖЈОЙ§вЛИіШЗЖЈВЛЖЏЕуQЃЎЧыжБНгаДГіИУВЛЖЏЕуQЕФзјБъЃЎ
ЁОД№АИЁП(1)1ЃЌ![]() ЃЛ(2)жЄУїМћНтЮіЃЛ(3)ЂйaЃН
ЃЛ(2)жЄУїМћНтЮіЃЛ(3)ЂйaЃН![]() ЃЌnЁн2ЃЛЂкQ(2ЃЌ2)ЃЎ
ЃЌnЁн2ЃЛЂкQ(2ЃЌ2)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉД§ЖЈЯЕЪ§ЗЈЧѓжБЯпBCНтЮіЪНЃЌжБЯпOAНтЮіЪНЃЌНтЗНГЬзщЧѓЕУЕуPзјБъЃЌД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпНтЮіЪНЃЌЛЏЮЊЖЅЕуЪНМДПЩЃЛ
ЃЈ2ЃЉгЩBЃЈ2ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉПЩЕУжБЯпyBC=-2x+2ЃЌНтЗНГЬзщЧѓЕУНЛЕуPзјБъЃЌДњШыХзЮяЯпНтЮіЪНМДПЩЧѓЕУaЃЌbЃЛХфЗНЗЈНЋХзЮяЯпНтЮіЪНЛЏЮЊЖЅЕуЪНМДПЩЕУЖЅЕузјБъЃЛ
ЃЈ3ЃЉЂйгЩy=ax2+bx+nЙ§ЕуAЃЈ2ЃЌ1ЃЉЃЌПЩЕУy=ax2+![]() ЃЈ1-n-4aЃЉx+nЃЌгыy=
ЃЈ1-n-4aЃЉx+nЃЌгыy=![]() x+nСЊСЂВЂЯћШЅyЃЌдйгЩХзЮяЯпгыжБЯпBCгаЮЈвЛНЛЕуCЃЌПЩЕУЁї=1-4a=0ЃЌНЋa=
x+nСЊСЂВЂЯћШЅyЃЌдйгЩХзЮяЯпгыжБЯпBCгаЮЈвЛНЛЕуCЃЌПЩЕУЁї=1-4a=0ЃЌНЋa=![]() ДњШыХзЮяЯпНтЮіЪНМДПЩЧѓЕУЖЅЕузнзјБъЃЛНјЖјПЩЧѓЕУnЕФЗЖЮЇЃЛ
ДњШыХзЮяЯпНтЮіЪНМДПЩЧѓЕУЖЅЕузнзјБъЃЛНјЖјПЩЧѓЕУnЕФЗЖЮЇЃЛ
ЂкгЩжБЯпBDЃКy=px-2pгыХзЮяЯпжЛгавЛИіНЛЕуЃЌПЩЕУn+2p=4ЃЌНјЖјПЩЧѓЕУDЃЈ4ЃЌ4-nЃЉЃЌдйЧѓЕУжБЯпCDНтЮіЪНЮЊy=![]() x+nЃЌМДПЩЕУЃКжБЯпCDБиЖЈОЙ§ЖЈЕуQЃЈ2ЃЌ2ЃЉЃЎ
x+nЃЌМДПЩЕУЃКжБЯпCDБиЖЈОЙ§ЖЈЕуQЃЈ2ЃЌ2ЃЉЃЎ
(1)ЁпnЃН1ЃЌB(2ЃЌ0)ЃЌ
ЁрC(0ЃЌ1)
ЩшжБЯпBCНтЮіЪНЮЊyЃНmx+nЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ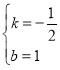 ЃЌ
ЃЌ
ЁржБЯпBCНтЮіЪНЮЊyЃН-![]() x+1ЃЌ
x+1ЃЌ
ЁпA(2ЃЌ1)ЃЌ
ЁржБЯпOAНтЮіЪНЮЊyЃН![]() xЃЌ
xЃЌ
НтЗНГЬзщ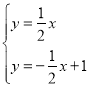 ЃЌЕУ
ЃЌЕУ![]() .
.
ЁрP(1ЃЌ![]() )ЃЌ
)ЃЌ
ЁпХзЮяЯпyЃНax2+bx+1(aЁй0ЃЌaЁйЉ1)ОЙ§AЃЌPЕуЃЌдђ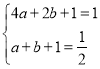 ЃЌНтЕУ
ЃЌНтЕУ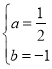
ЁрХзЮяЯпНтЮіЪНЮЊyЃН![]() Љx+1ЃН
Љx+1ЃН![]() (xЉ1)2+
(xЉ1)2+![]()
ЁрХзЮяЯпЖЅЕуЮЊP(1ЃЌ![]() )ЃЌ
)ЃЌ
ЙЪД№АИЮЊЃК1ЃЌ![]()
(2)гЩ(1)жЊЃКyOAЃН![]() xЃЌ
xЃЌ
гЩB(2ЃЌ0)ЃЌC(0ЃЌn)ПЩЕУжБЯпyBCЃН![]() x+n
x+n
ЕБnЃН2ЪБЃЌдђ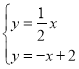 ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁрP(![]() ЃЌ
ЃЌ![]() )ЃЌ
)ЃЌ
НЋP(![]() ЃЌ
ЃЌ![]() )ЃЌA(2ЃЌ1)ДњШыyЃНax2+bx+2ЃЌЕУ
)ЃЌA(2ЃЌ1)ДњШыyЃНax2+bx+2ЃЌЕУ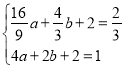 ЃЌНтЕУ
ЃЌНтЕУ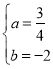 ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊyЃН![]() x2Љ2x+2ЃН
x2Љ2x+2ЃН![]() +
+![]()
ЁрЖЅЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЌМДЮЊPЕуЃЛ
)ЃЌМДЮЊPЕуЃЛ
(3)ЂйгЩyЃНax2+bx+nЙ§ЕуA(2ЃЌ1)ЃЌЕУ4a+2b+nЃН1ЃЌдђbЃН![]() (1ЉnЉ4a)ЃЌ
(1ЉnЉ4a)ЃЌ
ЁрyЃНax2+![]() (1ЉnЉ4a)x+n
(1ЉnЉ4a)x+n
СЊСЂЗНГЬзщ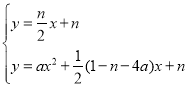 ЃЌЯћШЅyећРэЕУax2+
ЃЌЯћШЅyећРэЕУax2+![]() (1Љ4a)xЃН0ЃЌ
(1Љ4a)xЃН0ЃЌ
ИљОнЬтвтвЊХзЮяЯпгыжБЯпBCгаЮЈвЛНЛЕуCЃЌдђЁїЃН0ЃЌ
Ёр1Љ4aЃН0ЃЌ
ЁрaЃН![]() ЃЌ
ЃЌ
ДЫЪБЃЌХзЮяЯпЮЊЃКyЃН![]() =
=![]()
ЦфЖЅЕузнзјБъЮЊЃК![]() ЃЌ
ЃЌ
вЊCбиyжсЯђЩЯдЫЖЏЪБЃЌЦфЖЅЕуЭЌЪБЯђЯТдЫЖЏЃЌМДвЊЧѓЩЯЪНЫцnЕФдіДѓЖјМѕаЁЃЌ
ЁрnЁн2ЃЛ
ЂкЁпжБЯпBDНтЮіЪНЮЊyЃНpx+qЃЌНЋB(2ЃЌ0)ДњШыЕУ2p+qЃН0ЃЌ
ЁрqЃНЉ2p
ЁржБЯпBDНтЮіЪНЮЊyЃНpxЉ2p
СЊСЂЗНГЬзщ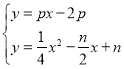 ЃЌЯћШЅyећРэЕУx2Љ2(n+2p)x+4(n+2p)ЃН0ЃЌ
ЃЌЯћШЅyећРэЕУx2Љ2(n+2p)x+4(n+2p)ЃН0ЃЌ
ИљОнЬтвтвЊХзЮяЯпгыжБЯпBDгаЮЈвЛНЛЕуCЃЌдђЁїЃН0ЃЌ
Ёр4(n+2p)2Љ16(n+2p)ЃН0ЃЌМД(n+2p)(n+2pЉ4)ЃН0
Ёпn+2pЁй0
Ёрn+2pЃН4
МДpЃН![]()
ЁржБЯпBDНтЮіЪНЮЊyЃН![]() x+nЉ4
x+nЉ4
ЁрD(4ЃЌ4Љn)
ЁпC(0ЃЌn)
ЁржБЯпCDНтЮіЪНЮЊyЃН![]() x+nЃЌЕБxЃН2ЪБЃЌyЃН
x+nЃЌЕБxЃН2ЪБЃЌyЃН![]() ЁС2+nЃН2
ЁС2+nЃН2
ЁржБЯпCDБиЖЈОЙ§ЖЈЕуQ(2ЃЌ2)ЃЎ

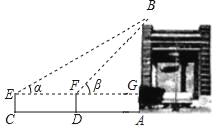
ЁОЬтФПЁПФГАрЪ§бЇЛюЖЏаЁзщВтСПМЊСжЪаЁАЪРМЭжЎжлЁБЕФИпЖШЃЎЫћУЧжЦЖЈСЫВтСПЗНАИЃЌВЂРћгУПЮгрЪБМфЭъГЩСЫЪЕЕиВтОАЃЌВтСПЯюФПМАЪ§ОнШчЯТБэЃК
ЯюФП | ФкШн | |||
ПЮЬт | ВтСПМЊСжЪаЁАЪЕМЪжЎжлЁБЕФИпЖШ | |||
ЪОвтЭМ |
| ШчЭМЃЌгУВтНЧвЧдк | ||
ВтСПЪ§Он |
|
|
| ВтНЧвЧ |
|
| 50Уз | 1.5Уз | |
Ё | Ё | |||
ЧыФуИљОнЛюЖЏаЁзщВтЕУЕФЪ§ОнЃЌЧѓЪРМЭжЎжлЕФИп![]() ЃЈНсЙћБЃСєаЁЪ§ЕуКѓвЛЮЛЃЉЃЎ
ЃЈНсЙћБЃСєаЁЪ§ЕуКѓвЛЮЛЃЉЃЎ
ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ