题目内容
【题目】已知:如图,在四边形ABCD中,AB=BC,AD2+CD2=2AB2,CD⊥AD.

(1)求证:AB⊥BC.
(2)若AB=3CD,AD=17,求四边形ABCD的周长.
【答案】(1)见解析;(2)17+7![]() .
.
【解析】
(1)由勾股定理的逆定理证明∠ABC=90°即可;
(2)设CD=k,则AB=BC=3k,由∠ABC=90°,可得AC2=18k2,在Rt△ACD中,根据AC2=CD2+AD2,构建方程即可解决问题.
(1)证明:连接AC.
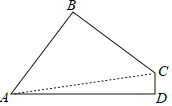
∵CD⊥AD,
∴AD2+CD2=AC2,
∵AD2+CD2=2AB2,AB=BC,
∴AC2=AB2+BC2,
∴∠ABC=90°,
∴AB⊥BC.
(2)设CD=k,则AB=BC=3k,
∵∠ABC=90°,
∴AC2=18k2,
在Rt△ACD中,∵AC2=CD2+AD2,
∴18k2=172+k2,
∴k=![]() ,
,
∴CD=![]() ,AB=BC=3
,AB=BC=3![]() ,
,
∴四边形ABCD的周长=AB+BC+AD+CD=17+7![]() .
.

练习册系列答案
相关题目
【题目】某班男同学身高情况如下表,则其中数据167cm( )
身高(cm) | 170 | 169 | 168 | 167 | 166 | 165 | 164 | 163 |
人数(人) | 1 | 2 | 5 | 8 | 6 | 3 | 3 | 2 |
A.是平均数B.是众数但不是中位数.
C.是中位数但不是众数D.是众数也是中位数