题目内容
【题目】(1)方法感悟:如图①,在正方形ABCD中,点E、F分别为DC、BC边上的点,且满足∠EAF=45°,连接EF.将△ADE绕点A顺时针旋转90°得到△ABG,易证△GAF≌△EAF,从而得到结论:DE+BF=EF.根据这个结论,若CD=6,DE=2,求EF的长.

(2)方法迁移:如图②,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论.
∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论.
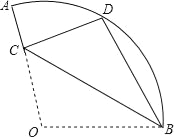
(3)问题拓展:如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由).
∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由).
【答案】(1)5;(2)EF= DE+BF;证明见解析;(3)EF=BE-FD
【解析】
(1)根据题意设![]() ,然后根据勾股定理得出x值进而求出
,然后根据勾股定理得出x值进而求出![]() 的长即可;
的长即可;
(2) 延长FB到G,使![]() ,连接AG,去根据已知条件证明
,连接AG,去根据已知条件证明![]() ,然后通过对应边的转化得出答案即可;
,然后通过对应边的转化得出答案即可;
(3)按照(1)的思路,我们应该通过全等三角形来实现相等线段的转换.就应该在BE上截取BG,使![]() ,连接AG.根据(1)的证法,我们可得出
,连接AG.根据(1)的证法,我们可得出![]() ,那么
,那么![]() .
.
解:(1)在正方形ABCD中,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
解得x=3,
![]()
(2)![]()
证明如下:
如图,延长FB到G,使![]() ,连接AG,
,连接AG,

![]()
![]() ,
,
在![]() 中,
中,
∵
![]()
![]()
![]()
![]()
在![]() 中,
中,
 ,
,
![]() ,
,
![]()
![]()
![]()
(3)结论:![]() ,
,
证明:如图所示,在BE上截取BG,使![]() ,连接AG.
,连接AG.
![]()
![]()
∵在![]() 中,
中, ,
,![]()
![]() .
.
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,
![]()
![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图1),然后拼成一个平行四边形(如图2)。那么通过计算两个图形的阴影部分的面积,可以验证成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |