题目内容
【题目】已知二次函数y=ax2+bx+c的图象如图所示，则在①a＜0，②b＞0，③c＜0，④b2﹣4ac＞0中错误的个数为（ ）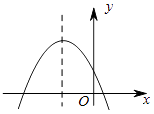
A.1
B.2
C.3
D.4
【答案】B
【解析】解：①∵抛物线开口向下，
∴a＜0，①正确；
②∵抛物线的对称轴在y轴左侧，
∴﹣ 
＜0，
∴b＜0，②错误；
③∵抛物线与y轴的交点在y轴的正半轴，
∴c＞0，③错误；
④∵抛物线与x轴有两个交点，
∴△=b2﹣4ac＞0，④正确．
综上所述：错误的结论有②③．
故B符合题意.
所以答案是：B．
【考点精析】掌握二次函数图象以及系数a、b、c的关系是解答本题的根本，需要知道二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】父亲告诉小明：“距离地面越高，温度越低”，并给小明出示了下面的表格：
距离地面高度（千米）h | 0 | 1 | 2 | 3 | 4 | 5 |
温度（℃）t | 20 | 14 | 8 | 2 | ﹣4 | ﹣10 |
根据表中，父亲还给小明出了下面几个问题，请你帮助小明回答下列问题:
（1）表中自变量是 ；因变量是 ；当地面上（即h=0时）时，温度是 ℃．
（2）如果用h表示距离地面的高度，用t表示温度，请写出满足t与h关系的式子．
（3）计算出距离地面6千米的高空温度是多少？
