题目内容
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


【答案】60
【解析】分析:(1)根据∠BAM+∠BAN=180°,∠BAM:∠BAN=2:1,即可得到∠BAN的度数;
(2)设A灯转动t秒,两灯的光束互相平行,分两种情况进行讨论:当0<t<90时,根据2t=1(30+t),可得 t=30;当90<t<150时,根据1(30+t)+(2t﹣180)=180,可得t=110;
(3)设灯A射线转动时间为t秒,根据∠BAC=2t﹣120°,∠BCD=120°﹣∠BCD=t﹣60°,即可得出∠BAC:∠BCD=2:1,据此可得∠BAC和∠BCD关系不会变化.
详解:(1)∵∠BAM+∠BAN=180°,∠BAM:∠BAN=2:1,∴∠BAN=180°×![]() =60°.
=60°.
故答案为:60;
(2)设A灯转动t秒,两灯的光束互相平行,
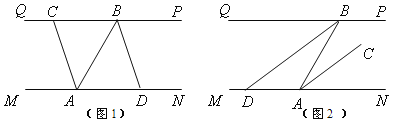
①当0<t<90时,如图1.
∵PQ∥MN,∴∠PBD=∠BDA.
∵AC∥BD,∴∠CAM=∠BDA,∴∠CAM=∠PBD
∴2t=1(30+t),解得 t=30;
②当90<t<150时,如图2.
∵PQ∥MN,∴∠PBD+∠BDA=180°.
∵AC∥BD,∴∠CAN=∠BDA
∴∠PBD+∠CAN=180°
∴1(30+t)+(2t﹣180)=180,解得 t=110.
综上所述:当t=30秒或110秒时,两灯的光束互相平行;
(3)∠BAC和∠BCD关系不会变化.
理由:设灯A射线转动时间为t秒,

∵∠CAN=180°﹣2t,∴∠BAC=60°﹣(180°﹣2t)=2t﹣120°.
又∵∠ABC=120°﹣t,∴∠BCA=180°﹣∠ABC﹣∠BAC=180°﹣t,而∠ACD=120°,∴∠BCD=120°﹣∠BCA=120°﹣(180°﹣t)=t﹣60°,∴∠BAC:∠BCD=2:1,即∠BAC=2∠BCD,∴∠BAC和∠BCD关系不会变化.

【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
某中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地校参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量 | 租金(元) | |
A | x | 45x | 400x |
B | 5﹣x |
|
|
(2)若要保证租车费用不超过1900元,求x的最大值.