��Ŀ����
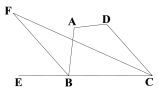
����Ŀ����Rt��ABC����C=90�㣬DΪAB����һ�㣬��M��N�ֱ���BC��AC���ϣ���DM��DN����MF��AB�ڵ�F��NE��AB�ڵ�E��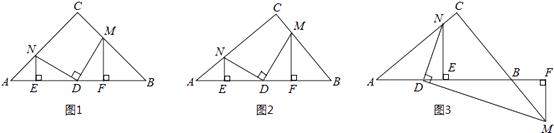
��1��������֤����ͼ1����AC=BC����DΪAB�е㣬��֤��DM=DN��AE=DF��
��2����չ̽������AC��BC��
����ͼ2����DΪAB�е㣬��1���е�����������һ���Գ�������ָ��������֤����
����ͼ3����BD=kAD�������С���M��BC���ϡ���Ϊ����M���߶�CB���ӳ����ϡ��������������䣬��̽��AE��DF��������ϵ������֤����
���𰸡�
��1��֤������AC=BC�����ABCΪ����ֱ�������Σ�

���ͼ1��ʾ������CD����CD��AB���֡�DM��DN�����1=��2��
�ڡ�AND���CMD�У� 
���AND�ա�CMD��ASA����
��DN=DM��
�ߡ�4+��1=90�㣬��1+��3=90�㣬���4=��3��
�ߡ�1+��3=90�㣬��3+��5=90�㣬���1=��5��
�ڡ�NED���DFM�У� 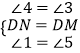
���NED�ա�DFM��ASA����
��NE=DF��
�ߡ�ANEΪ����ֱ�������Σ���AE=NE����AE=DF
��2���ٴ�AE=DF��
֤��һ���ɣ�1��֤����֪����DEN�ס�MFD
�� ![]() ����MFEN=DEDF��
����MFEN=DEDF��
ͬ����AEN�ס�MFB��
�� ![]() ����MFEN=AEBF��
����MFEN=AEBF��
��DEDF=AEBF��
�ࣨAD��AE��DF=AE��BD��DF����
��ADDF=AEBD����AE=DF��
֤���������ͼ2��ʾ������D��DP��BC�ڵ�P��DQ��AC�ڵ�Q��
��DΪAB�е㣬
��DQ=PC=PB��
��֤��DMF�ס�NDE���� ![]() ��
��
��֤��DMP�ס�DNQ���� ![]() ��
��
�� ![]() ��
��
��֤��AEN�ס�DPB���� ![]() ��
��
�� ![]() ����AE=DF��
����AE=DF��
�ڴ�DF=kAE��
֤��һ���ɢ�ͬ���ɵã�DEDF=AEBF��
�ࣨAE��AD��DF=AE��DF��BD��
��ADDF=AEBD
��BD=kAD
��DF=kAE��
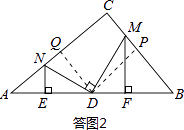
֤���������ͼ3������D��DP��BC�ڵ�P��DQ��AC�ڵ�Q��
��֤��AQD�ס�DPB���� ![]() ����PB=kDQ��
����PB=kDQ��
�ɢ�ͬ���ɵã� ![]() ��
��
�� ![]() ��
��
�֡� ![]() ��
��
�� ![]() ��
��
��DF=kAE
����������1������CD������֤����AND�ա�CMD������ȫ�������ε����ʿɵõ�DN=DM��Ȼ����֤����NED�ա�DFM���Ӷ��ɵõ�DF=NE��Ȼ�����ݵ��������ε����ʿɵõ�AE=NE=DF��
��2������DΪAB�е㣬���DEN�ס�MFD����AEN�ס�MFB��Ȼ���������������ε������г�����ʽ�������������߶α�����ϵ����֤��AE=DF������Ȼ����������BD=kAD��֤��˼·�������.
�����㾫�����������⣬������Ҫ�˽����������ε��ж�������(���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��)��

����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
=y2+8y+16 ���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ |
B��ƽ���ʽ |
C�������͵���ȫƽ����ʽ |
D�����������ȫƽ����ʽ |
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________�����������������������������������ף���ֱ��д����ʽ�ֽ�������_________ ��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮