Question

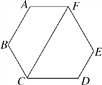
【题目】如图，六边形ABCDEF的内角都相等，CF∥AB.

(1)求∠FCD的度数；

(2)求证：AF∥CD.

Answer 1

【答案】（1）60°（2）证明见解析

【解析】试题分析：（1）先求六边形ABCDEF的每个内角的度数，根据平行线的性质可求∠B+∠BCF=180°，再根据四边形的内角和是360°，求∠FCD的度数，从而求解．
（2）先根据四边形内角和求出∠AFC=60°，再根据平行线的判定即可求解．

试题解析：(1)解：∵六边形ABCDEF的内角相等，∴∠B＝∠A＝∠BCD＝120°.

∵CF∥AB，∴∠B＋∠BCF＝180°，∴∠BCF＝60°，∴∠FCD＝60°.

(2)证明：∵CF∥AB，∴∠A＋∠AFC＝180°，∴∠AFC＝180°－120°＝60°，∴∠AFC＝∠FCD，∴AF∥CD.