题目内容
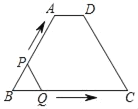
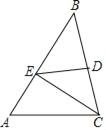
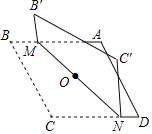
【题目】如图,直线l是线段MN的垂直平分线,交线段MN于点O,在MN下方的直线l上取一点P,连接PN,以线段PN为边,在PN上方作正方形NPAB,射线MA交直线l于点C,连接BC.
(1)设∠ONP=α,求∠AMN的度数;
(2)写出线段AM、BC之间的等量关系,并证明.
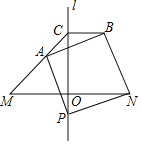
【答案】(1)45°(2)![]() ,理由见解析
,理由见解析
【解析】
(1)由线段的垂直平分线的性质可得PM=PN,PO⊥MN,由等腰三角形的性质可得∠PMN=∠PNM=α,由正方形的性质可得AP=PN,∠APN=90°,可得∠APO=α,由三角形内角和定理可求∠AMN的度数;
(2)由等腰直角三角形的性质和正方形的性质可得![]() ,
,![]() ,∠MNC=∠ANB=45°,可证△CBN∽△MAN,可得
,∠MNC=∠ANB=45°,可证△CBN∽△MAN,可得![]() .
.
解:(1)如图,连接MP,
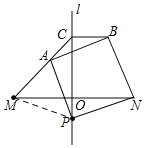
∵直线l是线段MN的垂直平分线,
∴PM=PN,PO⊥MN
∴∠PMN=∠PNM=α
∴∠MPO=∠NPO=90°-α,
∵四边形ABNP是正方形
∴AP=PN,∠APN=90°
∴AP=MP,∠APO=90°-(90°-α)=α
∴∠APM=∠MPO-∠APO=(90°-α)-α=90°-2α,
∵AP=PM
∴![]() ,
,
∴∠AMN=∠AMP-∠PMN=45°+α-α=45°
(2)![]()
理由如下:
如图,连接AN,CN,

∵直线l是线段MN的垂直平分线,
∴CM=CN,
∴∠CMN=∠CNM=45°,
∴∠MCN=90°
∴![]() ,
,
∵四边形APNB是正方形
∴∠ANB=∠BAN=45°
∴![]() ,∠MNC=∠ANB=45°
,∠MNC=∠ANB=45°
∴∠ANM=∠BNC
又∵![]()
∴△CBN∽△MAN
∴![]()
∴![]()

 寒假学与练系列答案
寒假学与练系列答案【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子频率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:①种子个数是700时,发芽种子的个数是624.所以种子发芽的概率是0.891;②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性.可以估计种子发芽的概率约为0.9(精确到0.1);③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子大约有
种子大约有![]() 的种子不能发芽.其中合理的是( )
的种子不能发芽.其中合理的是( )
A.①②B.③④C.②③D.②④