题目内容
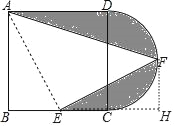
【题目】如图，在正方形ABCD中，AB=12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，图中阴影部分的面积是（ ）
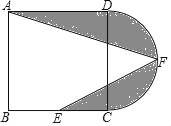
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
【答案】C
【解析】作FH⊥BC于H，连接FH，如图，根据正方形的性质和切线的性质得BE=CE=CH=FH=6，则利用勾股定理可计算出AE=6
，通过Rt△ABE≌△EHF得∠AEF=90°，然后利用图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF进行计算．
作FH⊥BC于H，连接FH，如图，
∵点E为BC的中点，点F为半圆的中点，
∴BE=CE=CH=FH=6，
AE=
=6，
易得Rt△ABE≌△EHF，
∴∠AEB=∠EFH，
而∠EFH+∠FEH=90°，
∴∠AEB+∠FEH=90°，
∴∠AEF=90°，
∴图中阴影部分的面积=S正方形ABCD+S半圆﹣S△ABE﹣S△AEF
=12×12+
π62﹣×12×6﹣6×6
=18+18π．
故选：C．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛，其预赛成绩如图：
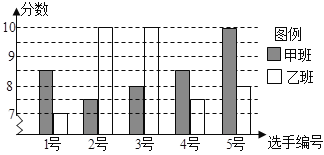
（1）根据上图求出下表中的a，b，c的值（单位：分）；
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
（2）学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛，求这5人预赛成绩的平均分数．
